题目内容
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
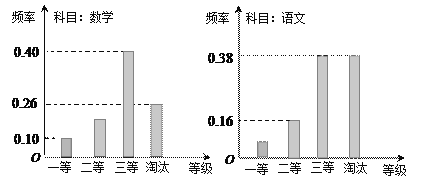

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
【答案】(Ⅰ)4人;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)由数学成绩为二等奖的考生人数及频率,可求得总人数,再利用对立事件的概率公式求出该考场考生中语文成绩为一等奖的频率,与总人数相乘即可得结果(Ⅱ)分别利用平均值公式与方差公式求出数学和语文二等奖的学生两科成绩的平均值与方差,可得数学二等奖考生较语文二等奖考生综合测试平均分高,但是稳定性较差;(Ⅲ)利用列举法求得随机抽取两人的基本事件个数为![]() 个,而两人两科成绩均为一等奖的基本事件共
个,而两人两科成绩均为一等奖的基本事件共![]() 个,利用古典概型概率公式可得结果.
个,利用古典概型概率公式可得结果.
试题解析:(Ⅰ)由数学成绩为二等奖的考生有![]() 人,可得
人,可得![]() ,所以语文成绩为一等奖的考生
,所以语文成绩为一等奖的考生![]() 人
人
(Ⅱ)设数学和语文两科的平均数和方差分别为![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
, ![]()
![]()
![]() ,因为
,因为![]() ,
,![]() ,所以数学二等奖考生较语文二等奖考生综合测试平均分高,但是稳定性较差.
,所以数学二等奖考生较语文二等奖考生综合测试平均分高,但是稳定性较差.
(Ⅲ)两科均为一等奖共有![]() 人,仅数学一等奖有
人,仅数学一等奖有![]() 人,仅语文一等奖有
人,仅语文一等奖有![]() 人----9分
人----9分
设两科成绩都是一等奖的![]() 人分别为
人分别为![]() ,只有数学一科为一等奖的
,只有数学一科为一等奖的![]() 人分别是
人分别是![]() ,只有语文一科为一等奖的
,只有语文一科为一等奖的![]() 人是
人是![]() ,则随机抽取两人的基本事件空间为
,则随机抽取两人的基本事件空间为![]()
![]()
![]() ,共有
,共有![]() 个,而两人两科成绩均为一等奖的基本事件
个,而两人两科成绩均为一等奖的基本事件![]() 共
共![]() 个,所以两人的两科成绩均为一等奖的概率
个,所以两人的两科成绩均为一等奖的概率![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目