题目内容
16.函数f(x)=x3+ax2+bx+a2(a>0)在x=1处的取得极值10,则a+b=-7.分析 利用已知条件列出方程组,求解即可.
解答 解:函数f(x)=x3+ax2+bx+a2,
可得f′(x)=3x2+2ax+b,
函数f(x)=x3+ax2+bx+a2(a>0)在x=1处的取得极值10,
可得:$\left\{\begin{array}{l}1+a+b+{a}^{2}=10\\ 3+2a+b=0\end{array}\right.$,解得a=4,b=-11或a=-3,b=3.
代回验证,a=-3 b=3时,函数取不到极值.
∴a+b=-7.
故答案为:-7.
点评 本题考查函数的导数的应用,函数的极值的求法,基本知识的考查.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6.设α,β,γ是三个互不重合的平面,m,n是两条不重合的直线,下列命题中正确的是( )
| A. | 若α⊥β,β⊥γ,则α⊥γ | B. | 若m∥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α⊥β,m?β,m⊥α,则m∥β | D. | 若α∥β,m∥α,则m∥β |
7.在等差数列{an}中公差d≠0,若a3+am-a7=an+a2-a5,则m-n=( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
11.已知平面向量$\overrightarrow{a},\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$,$\overrightarrow{b}$=(1,0)且$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则|2$\overrightarrow{a}$+$\overrightarrow{b}$|的值为( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{5}$ | D. | 5 |
5.若角α的终边落在直线y=3x上,则cosα的值为( )
| A. | ±$\frac{\sqrt{10}}{5}$ | B. | ±$\frac{\sqrt{10}}{10}$ | C. | ±$\frac{1}{3}$ | D. | ±$\frac{1}{5}$ |
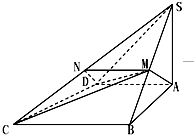 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.