题目内容
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是
是![]() 且边长为
且边长为![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() .
.

(1)若![]() 为
为![]() 边的中点,求证:
边的中点,求证:![]() 平面
平面![]() .
.
(2)求证:![]() .
.
(3)若![]() 为
为![]() 边的中点,能否在
边的中点,能否在![]() 上找出一点
上找出一点![]() ,使平面
,使平面 ![]() 平面
平面![]() ?
?
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)证明![]() ,利用面面垂直的性质即可证明(2)证
,利用面面垂直的性质即可证明(2)证![]() 平面
平面![]() 即可得
即可得![]() (3)存在点
(3)存在点![]() ,且
,且![]() 为
为![]() 的中点,证明
的中点,证明![]() 平面
平面![]() ,即可证出平面
,即可证出平面 ![]() 平面
平面![]() .
.
证明:连接![]() ,
,![]() ,
,

因为![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 边的中点,所以
边的中点,所以![]() .
.
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为四边形![]() 是菱形,所以
是菱形,所以![]() .又因为
.又因为![]() ,所以
,所以![]() 是等边三角形,所以
是等边三角形,所以![]() .又因为
.又因为![]() ,,所以
,,所以![]() 平
平![]() .
.
(2)证明:因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(3)存在点![]() ,且
,且![]() 为
为![]() 的中点.证明如下:连接
的中点.证明如下:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
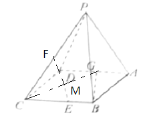
因为![]() 且
且![]() ,又
,又![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .又因为
.又因为![]() ,所以
,所以![]() .由(1)知
.由(1)知![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.

【题目】中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出10人,进行体育锻炼体会交流,
(i)求这10人中,男生、女生各有多少人?
(ii)从参加体会交流的10人中,随机选出2人作重点发言,记这2人中女生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |