题目内容
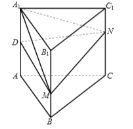
【题目】正三棱柱![]() (底面是正三角形,侧棱垂直底面)的各条棱长均相等,
(底面是正三角形,侧棱垂直底面)的各条棱长均相等,![]() 为
为![]() 的中点,
的中点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 、
、![]() 运动时,下列结论中正确的个数是( )
运动时,下列结论中正确的个数是( )
①平面![]() 平面
平面![]() ;
;
②三棱锥![]() 的体积为定值;
的体积为定值;
③![]() 可能为直角三角形;
可能为直角三角形;
④平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]() .
.
A.1B.2C.3D.4
【答案】C
【解析】
①由![]() 得线段MN必过正方形
得线段MN必过正方形![]() 的中心O,则
的中心O,则![]() 平面
平面![]() ,推出面面垂直;②由
,推出面面垂直;②由![]() 的面积不变,点N到平面
的面积不变,点N到平面![]() 的距离不变得到三棱锥
的距离不变得到三棱锥![]() 的体积为定值;③利用反证法说明
的体积为定值;③利用反证法说明![]() 不可能为直角三角形;④设三棱柱棱长为a,
不可能为直角三角形;④设三棱柱棱长为a,![]() ,建立空间直角坐标系,利用向量法表示出平面
,建立空间直角坐标系,利用向量法表示出平面![]() 与平面
与平面![]() 所成二面角的余弦值,根据t的范围求出
所成二面角的余弦值,根据t的范围求出![]() 的范围即可求得两平面所成锐二面角的范围.
的范围即可求得两平面所成锐二面角的范围.
①如图当M、N分别在![]() 、
、![]() 上运动时,若满足
上运动时,若满足![]() ,则线段MN必过正方形
,则线段MN必过正方形![]() 的中心O,而
的中心O,而![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,①正确;
,①正确;
②当M、N分别在![]() 、
、![]() 上运动时,
上运动时,![]() 的面积不变,点N到平面
的面积不变,点N到平面![]() 的距离不变,所以棱锥
的距离不变,所以棱锥![]() 的体积不变,即三棱锥
的体积不变,即三棱锥![]() 的体积为定值,②正确;
的体积为定值,②正确;
③设三棱柱棱长为a,![]() ,由
,由![]() 易知
易知![]() 且
且![]() ,
,![]() ,
,
若![]() 为直角三角形则
为直角三角形则![]() ,
,![]() ,
,
所以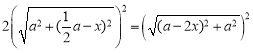 ,化简得
,化简得![]() ,
,
解得![]() 或
或![]() ,均不符合题意,所以
,均不符合题意,所以![]() 不可能为直角三角形,③错误;
不可能为直角三角形,③错误;
④建立如图所示空间直角坐标系:
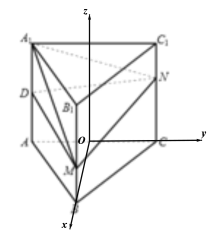
设三棱柱棱长为a,![]() ,则
,则![]() ,
,
![]() ,
,
设![]() 为平面DMN的法向量,则
为平面DMN的法向量,则
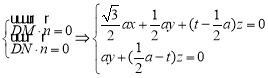 ,
,
令![]() 可得平面DMN的一个法向量为
可得平面DMN的一个法向量为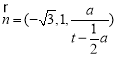 ,
,
易知![]() 为平面ABC的一个法向量,
为平面ABC的一个法向量,
设平面![]() 与平面
与平面![]() 所成二面角为
所成二面角为![]() ,则
,则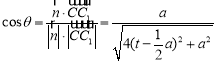 ,
,
因为![]() ,所以
,所以![]()
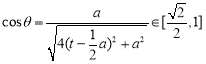 ,
,
所以平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]() ,④正确.
,④正确.
故选:C

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的60名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | 合计 | |
男生 | 20 | 10 | 30 |
女生 | 10 | 20 | 30 |
合计 | 30 | 30 | 60 |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选3人,求恰有2个男生和1个女生的概率.
下面的临界值表供参考:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)