题目内容
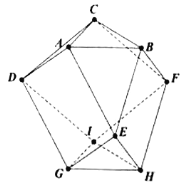
【题目】在如图所示的十一面体
中，用
种不同颜色给这个几何体各个顶点染色，每个顶点染一种颜色，要求每条棱的两端点异色，则不同的染色方案种数为__________．
【答案】6
【解析】分析：首先分析几何体的空间结构，然后结合排列组合计算公式整理计算即可求得最终结果.
详解：空间几何体由11个顶点确定，首先考虑一种涂色方法：
假设A点涂色为颜色CA，B点涂色为颜色CB，C点涂色为颜色CC，
由AC的颜色可知D需要涂颜色CB，
由AB的颜色可知E需要涂颜色CC，
由BC的颜色可知F需要涂颜色CA，
由DE的颜色可知G需要涂颜色CA，
由DF的颜色可知I需要涂颜色CC，
由GI的颜色可知H需要涂颜色CB，
据此可知，当△ABC三个顶点的颜色确定之后，其余点的颜色均为确定的，
用三种颜色给△ABC的三个顶点涂色的方法有
种，
故给题中的几何体染色的不同的染色方案种数为6.
练习册系列答案
相关题目
【题目】随着生活水平的提高，越来越多的人参与了潜水这项活动.某潜水中心调查了100名男性与100女性下潜至距离水面5米时是否耳鸣，下图为其等高条形图：
①绘出
列联表；
②根据列联表的独立性检验，能否在犯错误的概率不超过0.005的前提下认为耳鸣与性别有关系？
附：
，其中
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
