题目内容
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且其图象的一个对称轴为
,且其图象的一个对称轴为![]() ,将函数
,将函数![]() 图象上所有点的橫坐标缩小到原来的
图象上所有点的橫坐标缩小到原来的![]() 倍,再将图象向左平移
倍,再将图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.
的图象.
(1)求![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
(2)求函数![]() 在区间
在区间![]() 上的零点;
上的零点;
(3)对于任意的实数![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ,单调递增区间为
,单调递增区间为![]() ;
;
(2)![]() 、
、![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】
(1)由函数![]() 的最小正周期求出
的最小正周期求出![]() 的值,由图象的对称轴方程得出
的值,由图象的对称轴方程得出![]() 的值,从而可求出函数
的值,从而可求出函数![]() 的解析式;
的解析式;
(2)先利用图象变换的规律得出函数![]() 的解析式,然后在区间
的解析式,然后在区间![]() 上解方程
上解方程![]() 可得出函数
可得出函数![]() 的零点;
的零点;
(3)对![]() 分三种情况
分三种情况![]() 、
、![]() 、
、![]() 分类讨论,分析函数
分类讨论,分析函数![]() 在区间
在区间![]() 上的单调性,得出
上的单调性,得出![]() 和
和![]() ,可得出
,可得出![]() 关于
关于![]() 的表达式,再利用函数
的表达式,再利用函数![]() 的单调性得出函数
的单调性得出函数![]() 的最大值.
的最大值.
(1)由题意可知,![]() ,
,![]() .
.
令![]() ,即
,即![]() ,
,
即函数![]() 的图象的对称轴方程为
的图象的对称轴方程为![]() .
.
由于函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,则
,则![]() ,因此,
,因此,![]() .
.
函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
(2)将函数![]() 的图象上所有点的橫坐标缩小到原来的
的图象上所有点的橫坐标缩小到原来的![]() 倍,得到函数
倍,得到函数![]() .
.
再将所得函数的图象向左平移![]() 个单位长度,
个单位长度,
得到函数![]() .
.
令![]() ,即
,即![]() ,化简得
,化简得![]() ,
,
得![]() 或
或![]() .
.
由于![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() .
.
因此,函数![]() 在
在![]() 上的零点为
上的零点为![]() 、
、![]() 、
、![]() ;
;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,![]() ,由于
,由于![]() ,
,![]() ,
,
此时,![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,![]() ,由于
,由于![]() ,
,![]() ,
,
此时,![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() ,
,![]() ,
,
此时,![]() .
.
所以,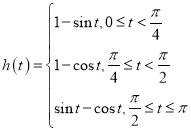 .
.
当![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() ;
;
当![]() 时,函数
时,函数![]() 单调递增,此时
单调递增,此时![]() ;
;
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
综上所述:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种产品的广告费用支出![]() (万元)与销售
(万元)与销售![]() (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
若由资料可知![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)据此估计广告费用支出为10万元时销售收入![]() 的值.
的值.
(参考公式:
 ,
,![]() .)
.)