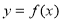题目内容
已知定义域为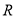 的函数
的函数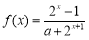 是奇函数.
是奇函数.
(1)求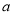 的值
的值
(2)判断并证明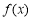 的单调性;
的单调性;
(3)若对任意的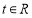 ,不等式
,不等式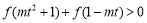 恒成立,求实数
恒成立,求实数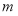 的取值范围.
的取值范围.
【解析】
试题分析:
(1)由题意可得函数的定义域是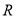 是奇函数,把
是奇函数,把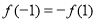 ,代入可得
,代入可得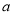 的值.
的值.
(2)直接利用函数单调性的定义进行判断,判断单调性的解题过程为做差,变形,判断符号,结论.
(3)由(1)可得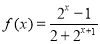 在它的定义域是
在它的定义域是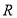 是减函数,且是奇函数,不等式化为
是减函数,且是奇函数,不等式化为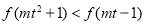 ,可得
,可得 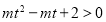 ,分
,分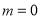 和
和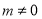 两种情况分别求出实数
两种情况分别求出实数 的取值范围
的取值范围
试题解析:(1) 由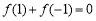 得
得
检验: 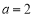 时,
时, 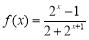

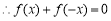 对
对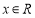 恒成立,即
恒成立,即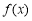 是奇函数.
是奇函数.
(2)判断:单调递增
证明:设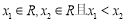 则
则
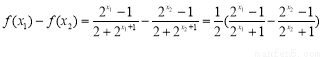
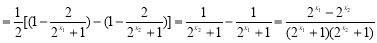
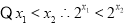 即
即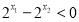
又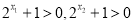 即
即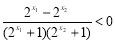 ,即
,即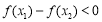 ,即
,即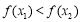
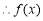 在
在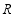 上是增函数
上是增函数
(3)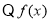 是奇函数
是奇函数
 不等式
不等式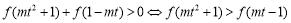
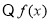 在
在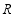 上是增函数
上是增函数
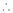 对任意的
对任意的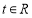 ,不等式
,不等式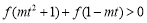 恒成立
恒成立
即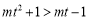 对任意的
对任意的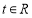 恒成立
恒成立
即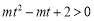 对任意的
对任意的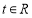 恒成立
恒成立
第一类:当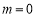 时,不等式即为
时,不等式即为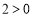 恒成立,合题意;
恒成立,合题意;
第二类:当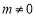 时,有
时,有 即
即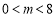
综上:实数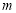 的取值范围为
的取值范围为
考点:本题主要考查函数的单调性和奇偶性的综合应用,函数的恒成立问题,考查了分类讨论的数学思想.

练习册系列答案
相关题目