题目内容
半径为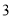
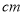 ,圆心角为
,圆心角为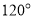 的扇形面积为
的扇形面积为 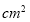 .
.
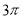
【解析】
试题分析:因为扇形面积为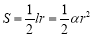 ,所以
,所以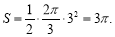 本题在运用公式求面积时需将圆心角化为弧度,这是与初中的扇形面积公式的区别.
本题在运用公式求面积时需将圆心角化为弧度,这是与初中的扇形面积公式的区别.
考点:扇形面积.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
题目内容
半径为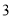
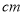 ,圆心角为
,圆心角为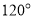 的扇形面积为
的扇形面积为 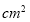 .
.
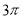
【解析】
试题分析:因为扇形面积为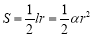 ,所以
,所以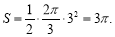 本题在运用公式求面积时需将圆心角化为弧度,这是与初中的扇形面积公式的区别.
本题在运用公式求面积时需将圆心角化为弧度,这是与初中的扇形面积公式的区别.
考点:扇形面积.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案