题目内容
((本小题满分12分)
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A( ,0),B(-
,0),B(- ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值- .
.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A(
 ,0),B(-
,0),B(- ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值- .
.(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
解:⑴由题意 ,----------- 2分
,----------- 2分
整理得 , 所以所求轨迹
, 所以所求轨迹 的方程为
的方程为 ,------ 4分
,------ 4分
⑵当直线 与
与 轴重合时,与轨迹
轴重合时,与轨迹 无交点,不合题意;
无交点,不合题意;
当直线 与
与 轴垂直时,
轴垂直时, ,此时
,此时 ,以
,以 为对角线的正方形的另外两个顶点坐标为
为对角线的正方形的另外两个顶点坐标为 ,不合题意;--------------- 6分
,不合题意;--------------- 6分
当直线 与
与 轴既不重合,也不垂直时,不妨设直线
轴既不重合,也不垂直时,不妨设直线 ,
,
 的中点
的中点 ,
,
由 消
消 得
得 ,
,
由 得
得 -------------------8分
-------------------8分
所以 ,
,
则线段 的中垂线
的中垂线 的方程为:
的方程为: ,
,
整理得直线 ,
,
则直线 与
与 轴的交点
轴的交点 ,
,
注意到以 为对角线的正方形的第三个顶点恰在
为对角线的正方形的第三个顶点恰在 轴上,
轴上,
当且仅当 ,
,
即 ,----------------10分
,----------------10分
 , ①
, ①
由 ②
②
将②代入①解得 ,即直线
,即直线 的方程为
的方程为 ,
,
综上,所求直线 的方程为
的方程为 或
或 .------------12分
.------------12分
 ,----------- 2分
,----------- 2分整理得
 , 所以所求轨迹
, 所以所求轨迹 的方程为
的方程为 ,------ 4分
,------ 4分⑵当直线
 与
与 轴重合时,与轨迹
轴重合时,与轨迹 无交点,不合题意;
无交点,不合题意;当直线
 与
与 轴垂直时,
轴垂直时, ,此时
,此时 ,以
,以 为对角线的正方形的另外两个顶点坐标为
为对角线的正方形的另外两个顶点坐标为 ,不合题意;--------------- 6分
,不合题意;--------------- 6分当直线
 与
与 轴既不重合,也不垂直时,不妨设直线
轴既不重合,也不垂直时,不妨设直线 ,
, 的中点
的中点 ,
,由
 消
消 得
得 ,
,由
 得
得 -------------------8分
-------------------8分所以
 ,
,则线段
 的中垂线
的中垂线 的方程为:
的方程为: ,
,整理得直线
 ,
,则直线
 与
与 轴的交点
轴的交点 ,
,注意到以
 为对角线的正方形的第三个顶点恰在
为对角线的正方形的第三个顶点恰在 轴上,
轴上,当且仅当
 ,
,即
 ,----------------10分
,----------------10分 , ①
, ①由
 ②
②将②代入①解得
 ,即直线
,即直线 的方程为
的方程为 ,
,综上,所求直线
 的方程为
的方程为 或
或 .------------12分
.------------12分略

练习册系列答案
相关题目
 的两个焦点,点P在双曲线上且满足∣P F1∣·∣P F2∣=32,则∠F1PF2是( )
的两个焦点,点P在双曲线上且满足∣P F1∣·∣P F2∣=32,则∠F1PF2是( ) )的椭圆被直线
)的椭圆被直线 截得的弦的中点横坐标为
截得的弦的中点横坐标为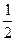 ,求此椭圆的方程。
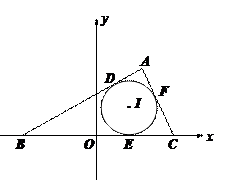
,求此椭圆的方程。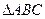 的内切圆与三边
的内切圆与三边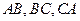 的切点分别为
的切点分别为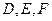 ,已知
,已知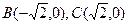 ,内切圆圆心
,内切圆圆心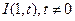 ,设点
,设点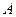 的轨迹为
的轨迹为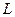 .
.
 的动直线
的动直线 交曲线
交曲线 (点
(点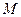 在
在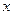 轴的上方),问在
轴的上方),问在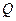 (
(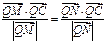 恒成立,若存在,试求出
恒成立,若存在,试求出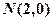 并且与圆
并且与圆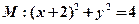 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线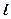 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。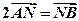 ,求直线
,求直线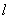 的方程;
的方程;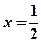 上是否存在一点Q,使得
上是否存在一点Q,使得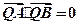 ,并说明理由。
,并说明理由。 和
和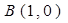 ,动点P到A、B两点距离之和为常数2,则动点P的轨迹是( )
,动点P到A、B两点距离之和为常数2,则动点P的轨迹是( ) 平面上两定点
平面上两定点 连线的斜率的积为定值
连线的斜率的积为定值 .
. 与曲线C交于M、N两点,求|MN|
与曲线C交于M、N两点,求|MN| 有共同的渐近线,且经过点
有共同的渐近线,且经过点 的双曲线的一个焦点到一条渐近线的距离是 ( )
的双曲线的一个焦点到一条渐近线的距离是 ( ) 中,
中, ,若周长为16,则顶点
,若周长为16,则顶点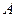 的轨迹方程为_________.
的轨迹方程为_________.