题目内容
(本小题满分12分)
已知动圆P过点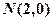 并且与圆
并且与圆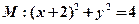 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线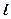 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。
(Ⅰ)求轨迹W的方程; (Ⅱ)若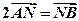 ,求直线
,求直线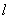 的方程;
的方程;
(Ⅲ)对于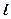 的任意一确定的位置,在直线
的任意一确定的位置,在直线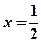 上是否存在一点Q,使得
上是否存在一点Q,使得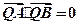 ,并说明理由。
,并说明理由。
已知动圆P过点
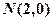 并且与圆
并且与圆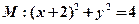 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线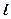 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。(Ⅰ)求轨迹W的方程; (Ⅱ)若
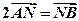 ,求直线
,求直线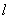 的方程;
的方程;(Ⅲ)对于
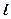 的任意一确定的位置,在直线
的任意一确定的位置,在直线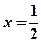 上是否存在一点Q,使得
上是否存在一点Q,使得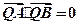 ,并说明理由。
,并说明理由。解:(Ⅰ)依题意可知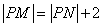 ∴
∴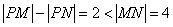 ,
,
∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为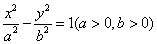 ,则
,则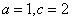 ∴
∴ ,∴轨迹W的方程为
,∴轨迹W的方程为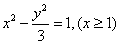
(Ⅱ)当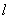 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足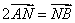 ,故
,故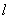 的斜率存在,设
的斜率存在,设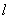 的方程为
的方程为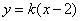 ,由
,由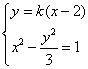 得
得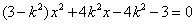 ,又设
,又设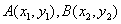 ,
,
则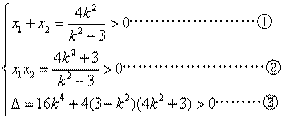 高#考#资#源#
高#考#资#源#
由①②③解得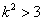 ,∵
,∵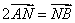 ∴
∴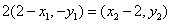
∴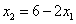 代入①②得
代入①②得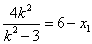 ,
,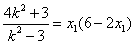
消去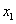 得
得 ,即
,即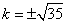 ,故所求直线
,故所求直线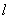 的方程为:
的方程为:
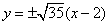 ;
;
(3)问题等价于判断以AB为直径的圆是否与直线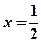 有公共点若直线
有公共点若直线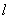 的斜率不存在,
的斜率不存在,
则以AB为直径的圆为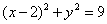 ,可知其与直线
,可知其与直线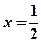 相交;
相交;
若直线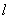 的斜率存在,则设直线
的斜率存在,则设直线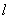 的方程为
的方程为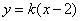 ,
,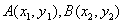
由(2)知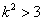 且
且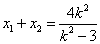 ,又
,又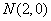 为双曲线的右焦点,
为双曲线的右焦点,
双曲线的离心率e=2,则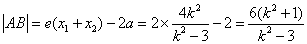
设以AB为直径的圆的圆心为S,点S到直径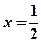 的距离为d,则
的距离为d,则
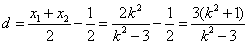 ∴
∴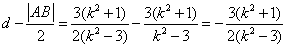
∵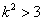 ∴
∴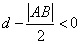 即
即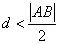 ,即直线
,即直线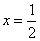 与圆S相交。
与圆S相交。
综上所述,以线段AB为直径的圆与直线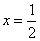 相交;
相交;
故对于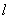 的
的 任意一确定的位置,
任意一确定的位置,
与直线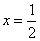 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得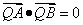
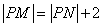 ∴
∴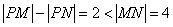 ,
,∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为
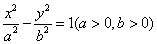 ,则
,则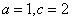 ∴
∴ ,∴轨迹W的方程为
,∴轨迹W的方程为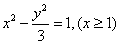
(Ⅱ)当
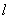 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足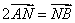 ,故
,故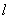 的斜率存在,设
的斜率存在,设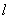 的方程为
的方程为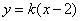 ,由
,由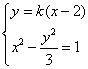 得
得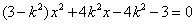 ,又设
,又设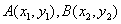 ,
,则
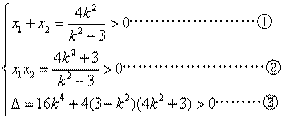 高#考#资#源#
高#考#资#源#由①②③解得
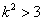 ,∵
,∵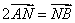 ∴
∴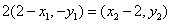
∴
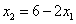 代入①②得
代入①②得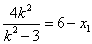 ,
,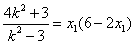
消去
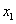 得
得 ,即
,即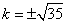 ,故所求直线
,故所求直线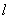 的方程为:
的方程为:
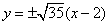 ;
;
(3)问题等价于判断以AB为直径的圆是否与直线
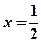 有公共点若直线
有公共点若直线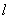 的斜率不存在,
的斜率不存在,则以AB为直径的圆为
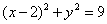 ,可知其与直线
,可知其与直线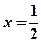 相交;
相交;若直线
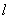 的斜率存在,则设直线
的斜率存在,则设直线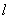 的方程为
的方程为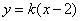 ,
,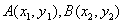
由(2)知
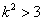 且
且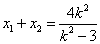 ,又
,又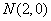 为双曲线的右焦点,
为双曲线的右焦点,双曲线的离心率e=2,则
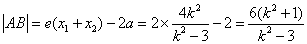
设以AB为直径的圆的圆心为S,点S到直径
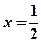 的距离为d,则
的距离为d,则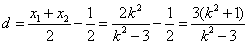 ∴
∴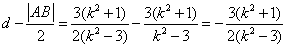
∵
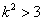 ∴
∴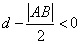 即
即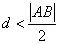 ,即直线
,即直线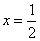 与圆S相交。
与圆S相交。综上所述,以线段AB为直径的圆与直线
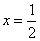 相交;
相交;故对于
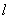 的
的 任意一确定的位置,
任意一确定的位置,与直线
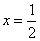 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得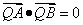
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 题满分14分)
题满分14分)  过点P(0,2), 且在
过点P(0,2), 且在 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.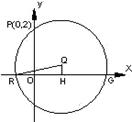
 点
点 (0,1),作轨迹
(0,1),作轨迹 的两条互相垂直的弦
的两条互相垂直的弦 ,设
,设 、
、 、
、 ,试判断直线
,试判断直线 是否过定点?并说明理由.
是否过定点?并说明理由. ,0),B(-
,0),B(- .
.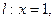 P是动点,作
P是动点,作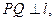 垂足为Q,且
垂足为Q,且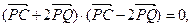 设P点的轨迹是曲线M。
设P点的轨迹是曲线M。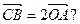 若存在,求出直线m的方程;若不存在,说明理由。
若存在,求出直线m的方程;若不存在,说明理由。 中,A、B两点的坐标分别是(-2,0)(2,0),AC、AB、BC成等差数列。
中,A、B两点的坐标分别是(-2,0)(2,0),AC、AB、BC成等差数列。 到点M(-1,0)的距离与点P到点N(1,0)的距离之比为
到点M(-1,0)的距离与点P到点N(1,0)的距离之比为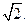
 ,求点N到
,求点N到 对称的曲线方程
对称的曲线方程 )
) ,求动点M的轨迹方程并指出轨迹是什么图形.
,求动点M的轨迹方程并指出轨迹是什么图形.