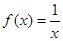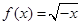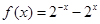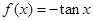题目内容
(本小题满分12分)探究函数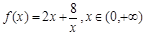 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数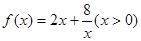 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数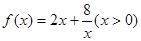 在区间 上递增.当
在区间 上递增.当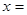 时,
时,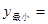 .
.
(2)证明:函数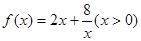 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考:函数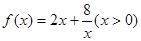 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
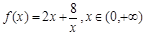 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数
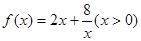 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数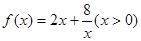 在区间 上递增.当
在区间 上递增.当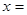 时,
时,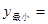 .
.(2)证明:函数
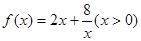 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
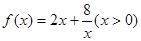 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)(1)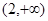 ;当
;当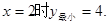
(2)证明:设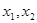 是区间,(0,2)上的任意两个数,且
是区间,(0,2)上的任意两个数,且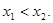
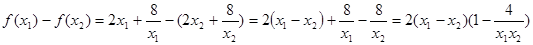
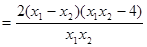
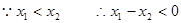
又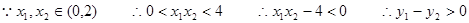
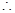 函数在(0,2)上为减函数.
函数在(0,2)上为减函数.
(3)思考: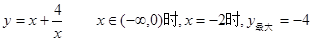 。
。
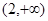 ;当
;当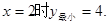
(2)证明:设
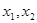 是区间,(0,2)上的任意两个数,且
是区间,(0,2)上的任意两个数,且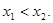
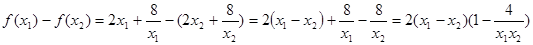
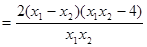
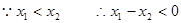
又
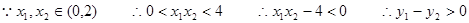
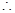 函数在(0,2)上为减函数.
函数在(0,2)上为减函数. (3)思考:
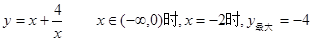 。
。试题分析:(1)
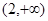 ;当
;当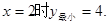 4分
4分(2)证明:设
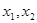 是区间,(0,2)上的任意两个数,且
是区间,(0,2)上的任意两个数,且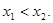
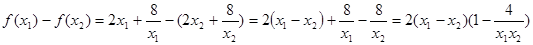
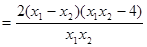
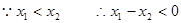
又
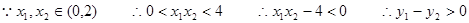
 函数在(0,2)上为减函数. 10分
函数在(0,2)上为减函数. 10分(3)思考:
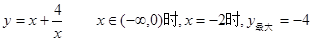 12分
12分点评:典型题,“对号函数”是高考常常考查的一类函数,其单调性及取得最值的情况又具有一般性,因此,学习中应倍加关注。

练习册系列答案
相关题目
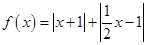 .
. 的图象,写出函数
的图象,写出函数 的不等式
的不等式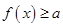
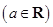 .
.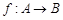 ,其中
,其中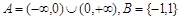 ,且对于
,且对于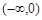 中的任意一个
中的任意一个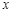 都与集合
都与集合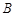 中的
中的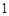 对应,
对应,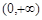 中的任意一个
中的任意一个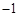 对应,则
对应,则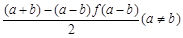 的值为( )
的值为( )
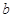
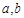 中较小的数
中较小的数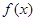 定义域为
定义域为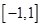 ,若对于任意的
,若对于任意的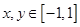 ,都有
,都有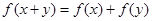 ,且
,且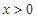 时,有
时,有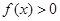 .
.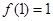 ,若
,若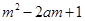 ,对所有
,对所有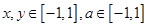 恒成立,求实数
恒成立,求实数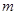 的取值范围.
的取值范围. ,
,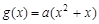
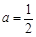 ,求
,求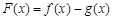 的单调区间;
的单调区间;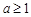 时,求证:
时,求证: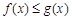 .
.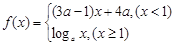 是(-
是(-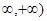 上的减函数,那么
上的减函数,那么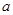 的取值范围是________
的取值范围是________ <ln(x+1)<x;
<ln(x+1)<x;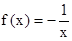 (2)
(2) (3)
(3)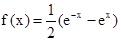
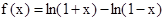 ,其中同时满足:①
,其中同时满足:①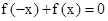 ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量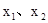 ,都有
,都有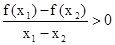 的函数个数为
的函数个数为