题目内容
设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: <ln(x+1)<x;
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式:
 <ln(x+1)<x;
<ln(x+1)<x;(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
(1) f(x)在(-1,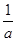 )为减,在(
)为减,在(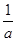 ,+
,+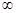 )为增
)为增
(2)将所证明的不等式利用构造函数,借助于导数的思想求解最值,来证明不等式恒大于等于零或者恒小于等于零即可。
(3)在上一问的基础上,进一步分析得到a的表达式,利用构造函数来求证。
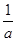 )为减,在(
)为减,在(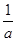 ,+
,+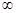 )为增
)为增(2)将所证明的不等式利用构造函数,借助于导数的思想求解最值,来证明不等式恒大于等于零或者恒小于等于零即可。
(3)在上一问的基础上,进一步分析得到a的表达式,利用构造函数来求证。
试题分析:解:(1)f’(x)=
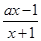 (x>-1,a>0)
(x>-1,a>0)令f’(x)=0
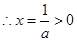
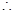 f(x)在(-1,
f(x)在(-1,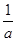 )为减,在(
)为减,在(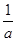 ,+
,+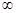 )为增 f (x)min=f(
)为增 f (x)min=f(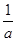 )=1-(a+1)ln(
)=1-(a+1)ln(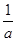 +1)
+1)(2)设F(x)=ln(x+1)-
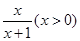
F’(x)=
 F(x)在(0,+
F(x)在(0,+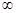 )为增函数
)为增函数F(x)>F(0)="0"
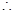 F(x)>0即
F(x)>0即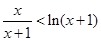
G(x)=x-ln(x+1)(x>0)
G’(x)=1-
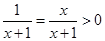
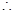 G(x)在(0,+
G(x)在(0,+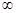 )为增函数
)为增函数G(x)>G(0)="0"
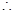 G(x)>0即ln(x+1)<x
G(x)>0即ln(x+1)<x经上可知
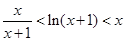
(3)由(1)知:
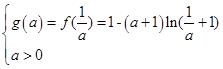
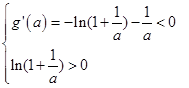
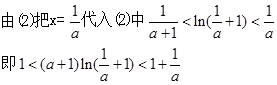
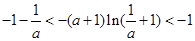
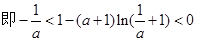
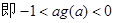
点评:导数在函数中的应用,频率最多的试题就是考查函数的单调性,以及证明不等式。那么对于后者的求解,关键是构造函数,借助于函数的最值来得到证明。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
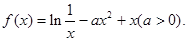
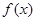 是定义域上的单调函数,求
是定义域上的单调函数,求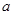 的取值范围;
的取值范围;
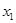 、
、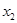 ,证明:
,证明: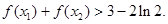
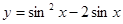 的值域是
的值域是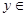 ;
;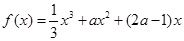 。
。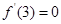 ,求a的值;
,求a的值;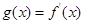 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m)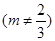 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。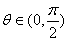 ,则函数
,则函数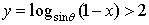 的解集是( )
的解集是( )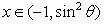
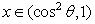
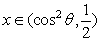
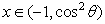
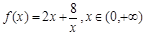 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下: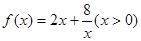 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数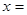 时,
时,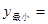 .
.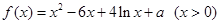
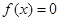 有三个不同的实根.
有三个不同的实根.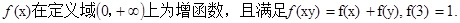
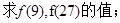
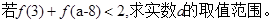
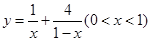 ,则
,则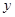 的最小值为 。
的最小值为 。