题目内容
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 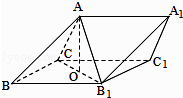
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
【答案】
(1)证明:连接BC1,则O为B1C与BC1的交点,
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,
∵AO⊥平面BB1C1C,
∴AO⊥B1C,
∵AO∩BC1=O,
∴B1C⊥平面ABO,
∵AB平面ABO,
∴B1C⊥AB
(2)解:作OD⊥BC,垂足为D,连接AD,作OH⊥AD,垂足为H,

∵BC⊥AO,BC⊥OD,AO∩OD=O,
∴BC⊥平面AOD,
∴OH⊥BC,
∵OH⊥AD,BC∩AD=D,
∴OH⊥平面ABC,
∵∠CBB1=60°,
∴△CBB1为等边三角形,
∵BC=1,∴OD= ![]() ,
,
∵AC⊥AB1,∴OA= ![]() B1C=
B1C= ![]() ,
,
由OHAD=ODOA,可得AD= ![]() =
= ![]() ,∴OH=
,∴OH= ![]() ,
,
∵O为B1C的中点,
∴B1到平面ABC的距离为 ![]() ,
,
∴三棱柱ABC﹣A1B1C1的高 ![]() .
.
【解析】(1)连接BC1 , 则O为B1C与BC1的交点,证明B1C⊥平面ABO,可得B1C⊥AB;(2)作OD⊥BC,垂足为D,连接AD,作OH⊥AD,垂足为H,证明△CBB1为等边三角形,求出B1到平面ABC的距离,即可求三棱柱ABC﹣A1B1C1的高.
【考点精析】认真审题,首先需要了解直线与平面垂直的性质(垂直于同一个平面的两条直线平行).

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目