题目内容
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
【答案】
(1)解:函数f(x)的定义域为(0,+∞), ![]()
当a=2时,f(x)=x﹣2lnx, ![]() ,
,
因而f(1)=1,f′(1)=﹣1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y﹣1=﹣(x﹣1),
即x+y﹣2=0
(2)解:由 ![]() ,x>0知:
,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0.
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a﹣alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a﹣alna,无极大值
【解析】(1)把a=2代入原函数解析式中,求出函数在x=1时的导数值,直接利用直线方程的点斜式写直线方程;(2)求出函数的导函数,由导函数可知,当a≤0时,f′(x)>0,函数在定义域(0,+∝)上单调递增,函数无极值,当a>0时,求出导函数的零点,由导函数的零点对定义域分段,利用原函数的单调性得到函数的极值.

【题目】函数f(x)的定义域为(﹣∞,a)∪(a,+∞),f(x)≥0的解集为M,f(x)<0的解集为N,则下列结论正确的是( )
A.M=CRN
B.CRM∩CRN=
C.M∪N=R
D.CRM∪CRN=R
【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
月份 | 2 | 3 | 4 | 5 |
产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图; 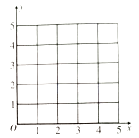
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量? (注:回归方程 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
= 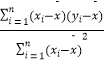 =
= 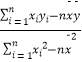 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)