题目内容
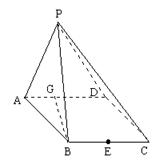
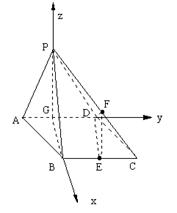
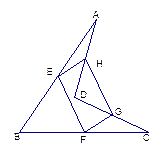
如图,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°且边长为1的菱形。侧面PAD是正三角形,其所在侧面垂直底面ABCD,G是AD中点。
(1)求异面直线BG与PC所成的角;
(2)求点G到面PBC的距离;
(3)若E是BC边上的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并说明理由。
(1)求异面直线BG与PC所成的角;
(2)求点G到面PBC的距离;
(3)若E是BC边上的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并说明理由。

(1)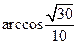 (2)
(2)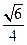 (3)F为PC中点
(3)F为PC中点
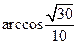 (2)
(2)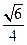 (3)F为PC中点
(3)F为PC中点 (1)∵△PAD为正三角形,G为AD中点,
∴PG⊥AD
又PG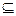 面PAD,面PAD⊥面ABCD
面PAD,面PAD⊥面ABCD
面PAD∩面ABCD=AD
∴PG⊥面ABCD,又GB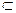 面ABCD
面ABCD
∴PG⊥GB
又∵∠DAB=60°,四边形ABCD为菱形,
∴BA=BD
∴BG⊥AD
以G为原点,GB所在直线为x轴,GD所在直线为y轴,GP所在直线为z轴,建立(如图所示)空间直角坐标系G—xyz,则G(0,0,0),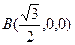 ,
, ,
,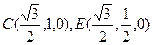
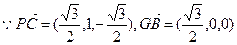
∴GB与PC所成角θ的余弦值为:
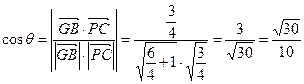
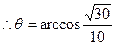
(2)设面PBC的一个法向量为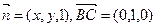
由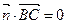 和
和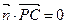 得
得
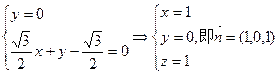
∴G到面PBC的距离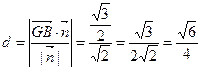
(3)设存在F点,使面DEF⊥面ABCD,且F分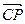 的比为
的比为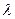
则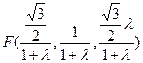
∵∠DAB=60°,∴BD=DC,又∵E为BC中点,∴BC⊥DE
由BC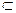 面ABCD,面DEF∩面ABCD=DE知
面ABCD,面DEF∩面ABCD=DE知
BC⊥面DEF
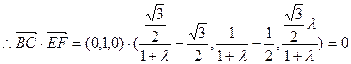
即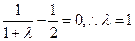
∴F为PC中点

∴PG⊥AD
又PG
 面PAD,面PAD⊥面ABCD
面PAD,面PAD⊥面ABCD面PAD∩面ABCD=AD
∴PG⊥面ABCD,又GB
 面ABCD
面ABCD∴PG⊥GB
又∵∠DAB=60°,四边形ABCD为菱形,
∴BA=BD
∴BG⊥AD
以G为原点,GB所在直线为x轴,GD所在直线为y轴,GP所在直线为z轴,建立(如图所示)空间直角坐标系G—xyz,则G(0,0,0),
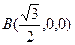 ,
, ,
,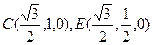
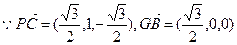
∴GB与PC所成角θ的余弦值为:
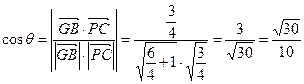
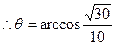
(2)设面PBC的一个法向量为
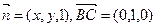
由
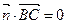 和
和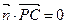 得
得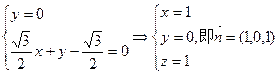
∴G到面PBC的距离
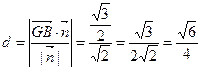
(3)设存在F点,使面DEF⊥面ABCD,且F分
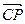 的比为
的比为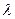
则
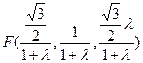
∵∠DAB=60°,∴BD=DC,又∵E为BC中点,∴BC⊥DE
由BC
 面ABCD,面DEF∩面ABCD=DE知
面ABCD,面DEF∩面ABCD=DE知BC⊥面DEF
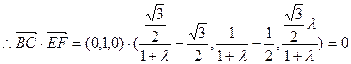
即
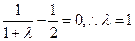
∴F为PC中点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,AC=3,BC=
,AC=3,BC= ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。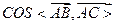 的值
的值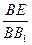 的值,不存在则说明理由。
的值,不存在则说明理由。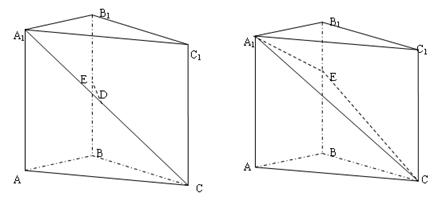
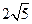 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
 中,
中, 、
、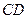 为底面圆的两条直径,
为底面圆的两条直径,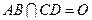 ,且
,且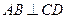 ,
,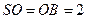 ,
,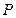 为
为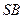 的中点.
的中点.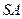 与
与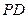 所成角的正切值.
所成角的正切值.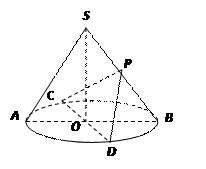
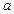 、
、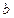 、
、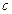 两两异面,空间与
两两异面,空间与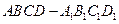 的棱
的棱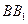 和
和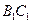 的中点,求:
的中点,求: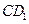 所成的角;
所成的角;
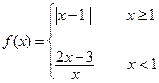 ,解不等式
,解不等式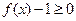 .
.