题目内容
见解析
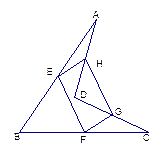
证明:连BD,在△ABC中,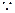 E,H是AB,AD的中点
E,H是AB,AD的中点
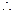 EH
EH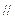 BD且EH=
BD且EH=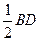 ,同理可证:FG∥BD且FG=
,同理可证:FG∥BD且FG=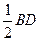
EH∥FG且EH="FG "
 四边形EFGH是平行四边形
四边形EFGH是平行四边形
 E,H是AB,AD的中点
E,H是AB,AD的中点 EH
EH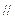 BD且EH=
BD且EH=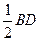 ,同理可证:FG∥BD且FG=
,同理可证:FG∥BD且FG=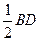
EH∥FG且EH="FG "
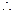 四边形EFGH是平行四边形
四边形EFGH是平行四边形
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
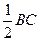 .
.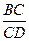 为何值时,有OF⊥ABE,试证明你的结论.
为何值时,有OF⊥ABE,试证明你的结论.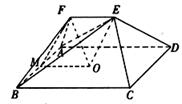
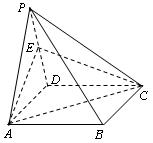
 中,
中, ,
, .
. ;
;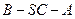 的大小.
的大小.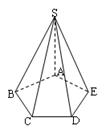
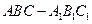 中,
中, ,
,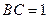 ,
,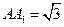 .
.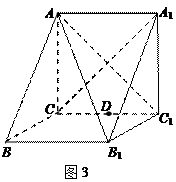
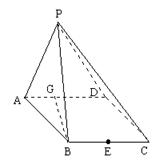
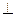 平面
平面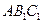 ;
;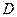 是棱
是棱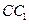 的中点,在棱
的中点,在棱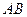 上是否存在一点
上是否存在一点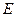 ,使
,使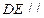 平面
平面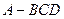 中,
中,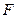 是
是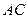 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H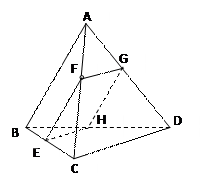
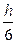 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。