题目内容
11.(1)求函数y=2x-3+$\sqrt{13-4x}$的值域(2)已知奇函数y=f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,求实数x的取值范围.
分析 (1)利用换元法求函数y=2x-3+$\sqrt{13-4x}$的值域
(2)利用奇函数y=f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,转化为具体的不等式,即可求实数x的取值范围.
解答 解:(1)设$\sqrt{13-4x}=t(t≥0)$,则$x=\frac{{13-{t^2}}}{4}$,…2分
原函数可化为$y=\frac{{13-{t^2}}}{2}-3+t=-\frac{1}{2}{(t-1)^2}+4\;\;\;(t≥0)$,
所以y≤4…5分
所以原函数的值域为(-∞,4]…7分
(2)由题意得$\left\{{\begin{array}{l}{-3<x-3<3}\\{-3<{x^2}-3<3}\end{array}}\right.$得 $0<x<\sqrt{6}$…9分
又因为f(x)是奇函数,
所以f(x-3)<-f(x2-3)=f(3-x2)…11分
又f(x)在(-3,3)上是减函数
所以 x-3>3-x2,即x2+x-6>0解得x>2或x<-3…13分
综上得$2<x<\sqrt{6}$…15分.
点评 本题考查函数的值域,考查单调性与奇偶性的综合,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
1.点p在曲线y=x3-x+3上移动,过点p的切线方程的倾斜角的取值范围有是( )
| A. | [0,π) | B. | [0,$\frac{π}{2}$)∪[$\frac{3}{4}$π,π) | C. | [0,$\frac{π}{2}$]∪($\frac{π}{2}$,$\frac{3}{4}$π] | D. | [0,$\frac{π}{4}$]∪[$\frac{3}{4}$π,π) |
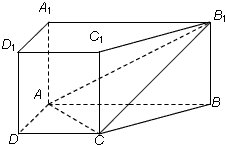 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.