题目内容
20.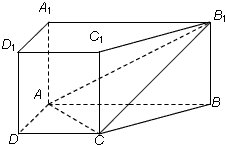 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.(1)建立适当的空间直角坐标系,并写出点A、C、B1的坐标.
(2)判断△ACB1是否为直角三角形?证明你的结论.
分析 (1)以A为原点,分别以AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,得到各点的坐标;
(2)利用(1)的结论得到△ACB1的三边对应的向量,利用数量积是否为0,判断三角形是否是直角三角形.
解答 解:(1)以A为原点,分别以AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,如图,
则A(0,0,0),C(1,1,0),B1(2,0,1);
(2)△ACB1为直角三角形;
证明:由(1)可知$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{A{B}_{1}}$=(2,0,1),$\overrightarrow{C{B}_{1}}$=(1,-1,1),所以$\overrightarrow{AC}•\overrightarrow{C{B}_{1}}$=0,所以$\overrightarrow{AC}⊥\overrightarrow{C{B}_{1}}$,
所以△ACB1为直角三角形.
点评 本题考查了利用空间向量解决空间直线的位置关系、判断三角形的形状;关键是正确建立空间直角坐标系,使问题向量化.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
8.过点A(2,3)且与抛物线y2=2x仅有一个交点的直线有( )条.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |