题目内容
【题目】在长方体ABCD﹣A1B1C1D1中，AB
，平面α过长方体顶点D，且平面α∥平面AB1C，平面α∩平面ABB1A1＝l，则直线l与BC1所成角的余弦值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由题意画出图形，得到平面α与平面ABB1A1的交线l，找出异面直线所成角，由已知结合余弦定理求解.
解：如图
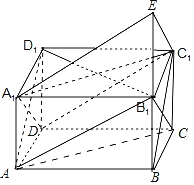
∵平面α过长方体顶点D，且平面α∥平面AB1C
∴平面α与平面A1DC1重合
在平面ABB1A1中，过A1作A1E∥AB1，则A1E∥DC1，即A1E为平面α与平面ABB1A1的交线l
连接AD1，可得AD1∥BC1，又l∥AB1，则∠D1AB1即为直线l与BC1所成角.
连接D1B1，由AB
，得
，
由余弦定理可得：cos∠D1AB1
.
即直线l与BC1所成角的余弦值为
.
故选：D
练习册系列答案
相关题目
