题目内容
．在正方体ABCD－A1B1C1D1中，直线A1B与平面BC1D1所成角的正切值为 （ ）
A． |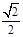
B． |
| C．1 |
D． |
B
建立空间直角坐标系，求出平面BC1D1的法向量，利用公式求出直线A1B与平面BC1D1所成的角的正弦值，然后求出正切值即可．
解：如图建立空间直角坐标系，设棱长为1，
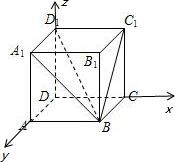
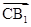是平面BC1D1的法向量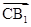，=（0，1，1）
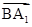=（-1，0，1）
直线A1B与平面BC1D1所成的角为α
sinα=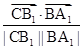
=
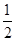
所以α=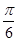
，tanα=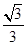
故选B．
解：如图建立空间直角坐标系，设棱长为1，
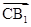是平面BC1D1的法向量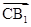，=（0，1，1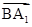）=（-1，0，1）直线A1B与平面BC1D1所成的角为α
sinα=
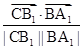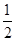
=所以α=
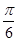，tanα=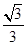故选B．
练习册系列答案
阅读快车系列答案
相关题目
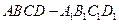中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．
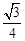
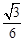
=3，那么直线AB与平面SBC所成角的正弦值为
点C在平面α外，AC和BC与平面α所成的角分别为300和450角，且平面ABC与平面α成600的锐二面角，则sin∠ACB＝（ ） 
中，
,则二面角
的平面角大小为