题目内容
在三棱锥P—ABC中,所有棱长均相等,若M为棱
AB的中点,则PA与CM所成角的余弦值为( )

AB的中点,则PA与CM所成角的余弦值为( )
A. | B.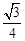  | C.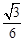 | D. |

C
本题采用几何法求异面直线所成的角,作辅助线,作出两线所成的角,再在三角形中求角即可
解:如图取PB中点N,连接MN与CN,
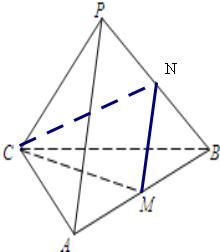
由题设条件M为棱AB的中点,故MN∥PA,故角NMC即为PA与CM所成角
∵三棱锥P-ABC中,所有棱长均相等不妨令棱长皆为2
∴MN= PA=1,CN=CM=
PA=1,CN=CM=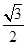 ×2=
×2=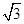
故cos∠CMN= =
=
故选C
解:如图取PB中点N,连接MN与CN,

由题设条件M为棱AB的中点,故MN∥PA,故角NMC即为PA与CM所成角
∵三棱锥P-ABC中,所有棱长均相等不妨令棱长皆为2
∴MN=
 PA=1,CN=CM=
PA=1,CN=CM=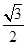 ×2=
×2=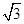
故cos∠CMN=
 =
=
故选C

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
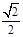



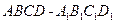 .(Ⅰ)求证:平面
.(Ⅰ)求证:平面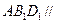 平面
平面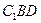 ;
;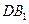 与
与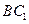 所成角的大小.
所成角的大小.
 ,b和c是两条异面直线.在下列给出的四个结论中,是“b和c所成的角为
,b和c是两条异面直线.在下列给出的四个结论中,是“b和c所成的角为 °
° ( )
( )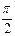

 中,
中, ,
, 与
与 所成角为
所成角为 ,则直线
,则直线 所成角的大小为_________.
所成角的大小为_________. 中,
中,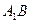 与平面
与平面 所成的角的大小是
所成的角的大小是 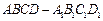 中,
中,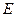 是棱
是棱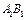 的中点,则
的中点,则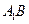 与
与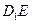 所成角的余弦值为( )
所成角的余弦值为( )


