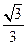题目内容
已知三棱锥S-ABC中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC, =3,那么直线AB与平面SBC所成角的正弦值为
=3,那么直线AB与平面SBC所成角的正弦值为
 =3,那么直线AB与平面SBC所成角的正弦值为
=3,那么直线AB与平面SBC所成角的正弦值为A. | B. | C. | D. |
D
专题:计算题.
分析:由图,过A作AE垂直于BC交BC于E,连接SE,过A作AF垂直于SE交SE于F,连BF,由题设条件证出∠ACF即所求线面角.由数据求出其正弦值.
解答:
 解:过A作AE垂直于BC交BC于E,连接SE,过A作AF垂直于SE交SE于F,连BF,
解:过A作AE垂直于BC交BC于E,连接SE,过A作AF垂直于SE交SE于F,连BF,∵正三角形ABC,
∴E为BC中点,
∵BC⊥AE,SA⊥BC,
∴BC⊥面SAE,
∴BC⊥AF,AF⊥SE,
∴AF⊥面SBC,
∵∠ABF为直线AB与面SBC所成角,由正三角形边长2,
∴AE=
 ,AS=3,
,AS=3,∴SE=2
 ,AF=
,AF= ,
,∴sin∠ABF=
 ;
;故选D.
点评:本题考查了立体几何的线与面、面与面位置关系及直线与平面所成角.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
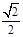



 ,b和c是两条异面直线.在下列给出的四个结论中,是“b和c所成的角为
,b和c是两条异面直线.在下列给出的四个结论中,是“b和c所成的角为
 中,
中, 的平面角;
的平面角; 面
面



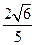

 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,
的中点, 所成的角的余弦值为
所成的角的余弦值为