题目内容
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)设![]() 为函数
为函数![]() 的导函数,求函数
的导函数,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 上有最大值,求实数
上有最大值,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(Ⅱ)
上单调递减;(Ⅱ)![]() .
.
【解析】
(Ⅰ)对函数求导,分![]() ,
,![]() 两种情况分析导函数正负;
两种情况分析导函数正负;
(Ⅱ)借助(Ⅰ)中单调性结论,分类讨论,当![]() 时,利用
时,利用![]() 放缩,
放缩,![]() ,分析即得解.
,分析即得解.
(Ⅰ)![]()
令![]() ,
,![]() ;
;
1°当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上递增,无减区间
上递增,无减区间![]()
2°当![]() 时,令
时,令![]() ,
,
令![]()
所以,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(Ⅱ)由(Ⅰ)可知,当![]() 时,∴
时,∴![]() 在(0,+∞)上递增,∴
在(0,+∞)上递增,∴![]()
∴![]() 在
在![]() 上递增,无最大值,不合题意;
上递增,无最大值,不合题意;
1°当![]() 时,
时,![]()
∴![]() 在
在![]() 上递减,∴
上递减,∴![]() ,
,
∴![]() 在
在![]() 上递减,无最大值,不合题意;
上递减,无最大值,不合题意;
2°当![]() 时,
时,![]() ,
,
由(Ⅰ)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
设![]() ,则
,则![]() ;
;
![]() ;令
;令![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增;
单调递增;
∴![]() ,即
,即![]()
由此,当![]() 时,
时,![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() .
.
取![]() ,则
,则![]() ,且
,且![]() .
.
又因为![]() ,所以由零点存在性定理,存在
,所以由零点存在性定理,存在![]() ,使得
,使得![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ;
;
所以,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上有最大值
上有最大值![]() .
.
综上,![]()

 口算能手系列答案
口算能手系列答案【题目】2019年12月16日,公安部联合阿里巴巴推出的“钱盾反诈机器人”正式上线,当普通民众接到电信网络诈骗电话,公安部钱盾反诈预警系统预警到这一信息后,钱盾反诈机器人即自动拨打潜在受害人的电话予以提醒,来电信息显示为“公安反诈专号”.某法制自媒体通过自媒体调查民众对这一信息的了解程度,从5000多参与调查者中随机抽取200个样本进行统计,得到如下数据:男性不了解这一信息的有50人,了解这一信息的有80人,女性了解这一信息的有40人.
(1)完成下列![]() 列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
了解 | 不了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)该自媒体对200个样本中了解这一信息的调查者按照性别分组,用分层抽样的方法抽取6人,再从这6人中随机抽取3人给予一等奖,另外3人给予二等奖,求一等奖与二等奖获得者都有女性的概率.
附:![]()
P(K2≥k) | 0.01 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
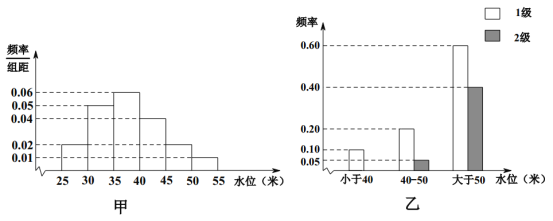
(1)试估计该河流在8月份水位的众数;
(2)我们知道若该河流8月份的水位小于40米的频率为f,该河流8月份的水位小于40米的情况下发生1级灾害的频率为g,则该河流8月份的水位小于40且发生1级灾害的频率为![]() ,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率
,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率![]() ,
,![]() ,
,![]() ;
;
(3)该河流域某企业,在8月份,若没受12级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.

