题目内容
设点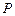 是椭圆
是椭圆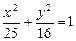 上一动点,
上一动点,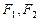 是椭圆的两个焦点,
是椭圆的两个焦点,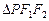 的内切圆半径为
的内切圆半径为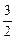 ,则当点点
,则当点点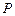 在
在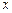 轴上方时,点
轴上方时,点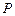 的纵坐标为( )
的纵坐标为( )
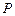 是椭圆
是椭圆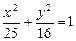 上一动点,
上一动点,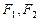 是椭圆的两个焦点,
是椭圆的两个焦点,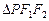 的内切圆半径为
的内切圆半径为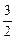 ,则当点点
,则当点点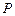 在
在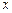 轴上方时,点
轴上方时,点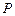 的纵坐标为( )
的纵坐标为( )| A.2 | B.4 | C.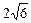  | D.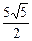 |
B
略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
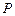 是椭圆
是椭圆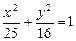 上一动点,
上一动点,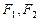 是椭圆的两个焦点,
是椭圆的两个焦点,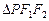 的内切圆半径为
的内切圆半径为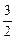 ,则当点点
,则当点点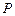 在
在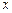 轴上方时,点
轴上方时,点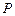 的纵坐标为( )
的纵坐标为( )| A.2 | B.4 | C.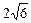  | D.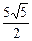 |

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案