题目内容
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 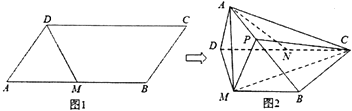
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
【答案】证明:(Ⅰ)连接OA,ON,因为AB=2AD,∠DAB=60°,M是BC的中点,
∴△ADM是正三角形,取DM的中点O,则AO⊥DM,
∵面ADM⊥面MBCD,∴AO⊥平面MBCD,
∵MC平面MBCD,∴AO⊥MC,
连接ON,△DMN为正三角形,
O是MD中点,ON⊥DM,ON为△DMC的中位线,
∴ON∥MC,故MC⊥DM,AO∩DM=O
∴CM⊥平面ADM
解:(Ⅱ)由(Ⅰ)可知,AO⊥DM,ON⊥DM,
以O为坐标原点,以OM,ON,OA方向为x,y,z轴的正方向,
建立空间直角坐标系O﹣xyz如图所示,
不妨设AB=2AD=2,
则 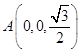 ,B(1,
,B(1, ![]() ,0),M(
,0),M( ![]() ,0,0),C(
,0,0),C( ![]() ),
),
则 ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() ),
),
设 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),(0<λ<1),
),(0<λ<1),
得 ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(0,
=(0, ![]() ,0),
,0),
设 ![]() =(x,y,z)为平面MCP的一个法向量,则有
=(x,y,z)为平面MCP的一个法向量,则有 ![]() =0,
=0, ![]() =0,
=0,
即 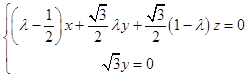 ,令x=1,得,
,令x=1,得, ![]()
∴ ![]() =(1,0,
=(1,0, ![]() ),
),
由意 ![]() =(0,0,1)为平面BMC的一个法向量,
=(0,0,1)为平面BMC的一个法向量,
∵二面角P﹣MC﹣B的大小为60°,
∴cos60°=  =
= 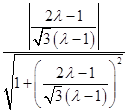 =
= ![]() ,
,
解得 ![]() ,
,
当 ![]() 时,二面角P﹣MC﹣B的大小为60°.
时,二面角P﹣MC﹣B的大小为60°.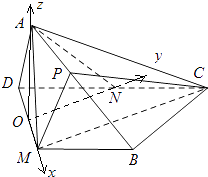
【解析】(Ⅰ)连接OA,ON,推导出AO⊥DM,AO⊥平面MBCD,AO⊥MC,连接ON推导出ON∥MC,由此能证明CM⊥平面ADM.(Ⅱ)以O为坐标原点,以OM,ON,OA方向为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,利用向量法能求出当 ![]() 时,二面角P﹣MC﹣B的大小为60°.
时,二面角P﹣MC﹣B的大小为60°.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案