题目内容
(1)如果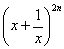 展开式中,第四项与第六项的系数相等。求
展开式中,第四项与第六项的系数相等。求 ,并求展开式中的常数项;
,并求展开式中的常数项;
(2)求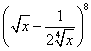 展开式中的所有的有理项。
展开式中的所有的有理项。
(1)70 (2)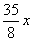
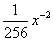
解析试题分析:(1)由C2n3=C2n5,可得3+5=2n∴ n=4。
设第k+1项为常数项,则 Tk+1=C8k·x8-k·x-k=C8k·x8-2k
∴8-2k=0,即k=4∴常数项为T5=C84=70.
(2)设第k+1项有理项,则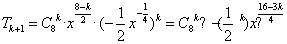
因为0≤k≤8,要使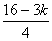 ∈Z,只有使k分别取0,4,8
∈Z,只有使k分别取0,4,8
所以所求的有理项应为:T1=x4,T5= x,T9=
x,T9=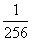 x-2
x-2
考点:二项式系数的性质;二项式定理的应用.
点评:本题考查二项式系数的性质,二项式展开式的通项公式,求出n值,是解题的关键.

练习册系列答案
相关题目
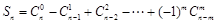 ,
,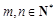 且
且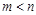 ,其中当
,其中当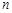 为偶数时,
为偶数时,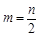 ;当
;当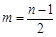 .
.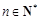 ,
,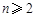 时,
时,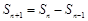 ;
;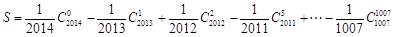 ,求
,求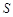 的值.
的值.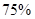 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.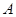 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为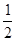 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
 的展开式中偶数项二项式系数和比
的展开式中偶数项二项式系数和比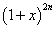 展开式中奇数项二项式系数和小
展开式中奇数项二项式系数和小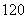 ,求:
,求: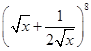 的展开式中,求
的展开式中,求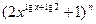 展开式中最后三项的系数的和是方程
展开式中最后三项的系数的和是方程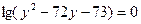 的正数解,它的中间项是
的正数解,它的中间项是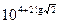 ,求
,求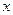 的值.
的值.