题目内容
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取5人.若从这5人中随机选取3人到火车站迎接新生,求选取的3人中恰好有1名女生的概率.
附: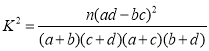 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)有;(2)![]()
【解析】
(1)利用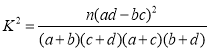 计算得到观察值
计算得到观察值![]() ,通过与临界值
,通过与临界值![]() 比较大小得出有99%把握认为愿意参加新生接待工作与性别有关;
比较大小得出有99%把握认为愿意参加新生接待工作与性别有关;
(2)根据分层抽样方法得出抽取男生有3人,女生有2人,分别记3名男生为a,b,c;2名女生为m,n.列出随机选取3人到火车站迎接新生的所有情况以及3人中恰好有1名女生的情况,然后根据古典概率公式计算概率.
解:(1)由公式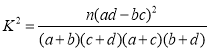 得:
得:
观测值![]() ,所以有
,所以有![]() 的把握认为愿意参加新生接待工作与性别有关
的把握认为愿意参加新生接待工作与性别有关
(2)根据分层抽样方法得:男生有![]() 人,女生有
人,女生有![]() 人,选取的5人中,男生有3人,女生有2人,分别记3名男生为a,b,c;2名女生为m,n.则从5人中任选3人的所有可能结果为:abc、abm、abn、acm、acn、bcm、bcn、amn、bmn、cmn.记选取的3人中恰好有1名女生为事件A,则
人,选取的5人中,男生有3人,女生有2人,分别记3名男生为a,b,c;2名女生为m,n.则从5人中任选3人的所有可能结果为:abc、abm、abn、acm、acn、bcm、bcn、amn、bmn、cmn.记选取的3人中恰好有1名女生为事件A,则![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
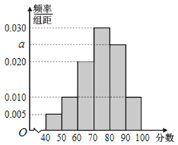
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: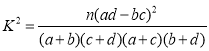 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
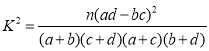 ,
,![]() .
.