题目内容
如图所示棱锥P—ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=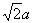 ,且PD是四棱锥的高.
,且PD是四棱锥的高.

(1)在这个四棱锥中放入一个球,求球的最大半径;
(2)求四棱锥外接球的半径.
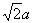 ,且PD是四棱锥的高.
,且PD是四棱锥的高. 
(1)在这个四棱锥中放入一个球,求球的最大半径;
(2)求四棱锥外接球的半径.
(1)球的最大半径为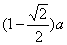 .(2)四棱锥外接球的半径为
.(2)四棱锥外接球的半径为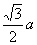 .
.
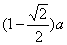 .(2)四棱锥外接球的半径为
.(2)四棱锥外接球的半径为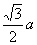 .
. (1)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连结SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R.
VP—ABCD=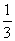 ·SABCD·PD=
·SABCD·PD=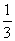 ·a·a·a=
·a·a·a=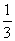 a3,
a3,
S△PAD=S△PDC=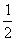 ·a·a=
·a·a=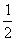 a2,
a2,
S△PAB=S△PBC=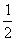 ·a·
·a·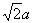 =
=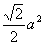 ,
,
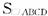 =a2.
=a2.
VP—ABCD=VS—PDA+VS—PDC+VS—ABCD+VS—PAB+VS—PBC,
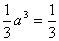 R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
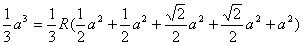
所以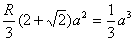 ,
,
 ,
,
即球的最大半径为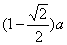 .
.
(2)设PB的中点为F.
因为在Rt△PDB中,FP=FB=FD,
在Rt△PAB中,FA=FP=FB,
在Rt△PBC中,FP=FB=FC,
所以FP=FB=FA=FC=FD.
所以F为四棱锥外接球的球心,
则FP为外接球的半径.
因为FB=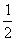 PB,所以FB=
PB,所以FB=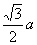 .
.
所以四棱锥外接球的半径为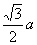 .
.
VP—ABCD=
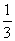 ·SABCD·PD=
·SABCD·PD=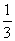 ·a·a·a=
·a·a·a=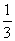 a3,
a3,S△PAD=S△PDC=
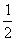 ·a·a=
·a·a=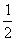 a2,
a2,S△PAB=S△PBC=
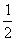 ·a·
·a·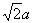 =
=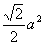 ,
,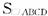 =a2.
=a2.VP—ABCD=VS—PDA+VS—PDC+VS—ABCD+VS—PAB+VS—PBC,
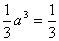 R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),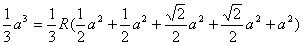
所以
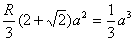 ,
, ,
,即球的最大半径为
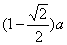 .
.(2)设PB的中点为F.
因为在Rt△PDB中,FP=FB=FD,
在Rt△PAB中,FA=FP=FB,
在Rt△PBC中,FP=FB=FC,
所以FP=FB=FA=FC=FD.
所以F为四棱锥外接球的球心,
则FP为外接球的半径.
因为FB=
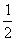 PB,所以FB=
PB,所以FB=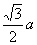 .
.所以四棱锥外接球的半径为
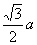 .
.
练习册系列答案
相关题目
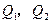 ,求直平行六面体的侧面积.
,求直平行六面体的侧面积. cm2
cm2 cm2
cm2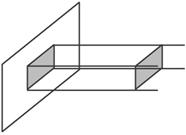
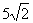
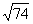
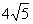
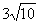
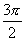
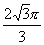
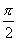
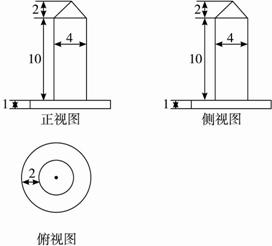
 ,求三棱锥的内切球的体积.
,求三棱锥的内切球的体积. 
 的底面边长和各侧棱长都为
的底面边长和各侧棱长都为 ,点S、A、B、C、D都在同一个球面上,则该球的体积为_________。
,点S、A、B、C、D都在同一个球面上,则该球的体积为_________。