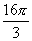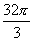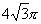题目内容
如图所示,三棱锥A-BCD的两条棱长AB=CD=6,其余各棱长均为5,此三棱锥的体积为
,求三棱锥的内切球的体积. 
,求三棱锥的内切球的体积. V球=
.
.设O为三棱锥内切球的球心,?
连结OA1、OB、OC、OD,?
则三棱锥A-BCD被分割成四个小三棱锥,?
即三棱锥O-ABC,三棱锥O-BCD,三棱锥O-ACD,三棱锥O-ABD,?
且每个小三棱锥的高均等于三棱锥ABCD的内切球的半径r.?
根据题意,AB=CD=6,?
三棱锥A-BCD的其余棱长均为5,?
得到三棱锥A-BCD的各面全等,且面积均为12,?
∴三棱锥A-BCD的体积V=V O-ABC+V O-BCD+V O-ACD+V O-ABD??
=
.?
又V=,∴=16r.
∴r=
.?∴V球=.
连结OA1、OB、OC、OD,?
则三棱锥A-BCD被分割成四个小三棱锥,?
即三棱锥O-ABC,三棱锥O-BCD,三棱锥O-ACD,三棱锥O-ABD,?
且每个小三棱锥的高均等于三棱锥ABCD的内切球的半径r.?
根据题意,AB=CD=6,?
三棱锥A-BCD的其余棱长均为5,?
得到三棱锥A-BCD的各面全等,且面积均为12,?
∴三棱锥A-BCD的体积V=V O-ABC+V O-BCD+V O-ACD+V O-ABD??
=
.?又V=
,∴=16r.∴r=
.?∴V球=.
练习册系列答案
相关题目
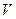表示为
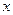的函数．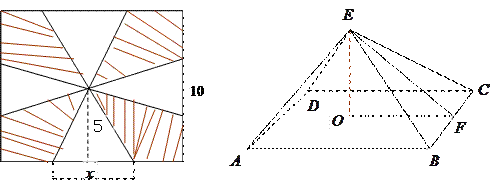
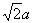，且PD是四棱锥的高． 
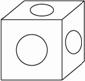
中，
，
，
，
，
，
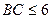．则三棱锥
