题目内容
2.$(3\frac{3}{8})^{-\frac{2}{3}}-(5\frac{4}{9})^{0.5}+$$(0.008)^{-\frac{2}{3}}×(0.02)^{\frac{1}{2}}$×$(0.32)^{\frac{1}{2}}$=$\frac{1}{3}$.分析 利用指数幂的运算性质即可得出.
解答 解:原式=$(\frac{3}{2})^{3×(-\frac{2}{3})}$-$(\frac{7}{3})^{2×0.5}$+$0.{2}^{3×(-\frac{2}{3})}$×$(0.08)^{2×\frac{1}{2}}$
=$\frac{2}{3}-\frac{7}{3}$+25×0.08
=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了指数幂的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
17.实系数一元二次方程x2+ax+2b=0的一个根在(0,1)上,另一个根在(1,2)上,则$\frac{b-3}{a-1}$的取值范围是( )
| A. | [1,3] | B. | (1,3) | C. | $[{\frac{1}{2},\frac{3}{2}}]$ | D. | $({\frac{1}{2},\frac{3}{2}})$ |
11.设函数y=3x与y=2-x的图象交点为(x0,y0),则x0所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
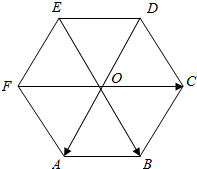 如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.
如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.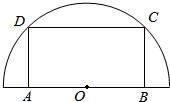 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.