题目内容

7．若函f（x）是定义域为R的奇函数，且f（x）在（0，+∞）上有一个零点．则f（x）的零点个数为（　　）
A．1B．2C．3D．4

分析 根据定义域为R的奇函数图象过零点，且函数图象关于原点对称，可得答案．

解答 解：∵函数f（x）是定义域为R的奇函数，
∴f（0）=0，
又∵f（x）在（0，+∞）上有一个零点．
∴f（x）在（-∞，0）上有一个零点．
综上所述，f（x）的零点个数为3个，
故选：C．

点评 本题考查的知识点是函数零点，函数的奇偶性，难度不大，属于基础题．

练习册系列答案
相关题目
14．已知函数f（x）=x2+ax+b，f（1）=0，f（2）=1
（1）求f（x）的解析式．
（2）求函数f（x）在区间[t，2t]上的最大值和最小值．
18．$\frac{（2sin20°-cos10°）}{sin10°}$+$\frac{sin50°（1+\sqrt{3}tan10°）-cos20°}{cos80°\sqrt{1-cos20°}}$=$\sqrt{2}-\sqrt{3}$．
15．函数f（x）=$\left\{\begin{array}{l}a{x^2}+x-1（x＞2）\\ ax-1（x≤2）\end{array}$是R上的单调递减函数，则实数a的取值范围是（　　）
A．-$\frac{1}{4}$≤a＜0B．a≤-$\frac{1}{4}$C．-1≤a≤-$\frac{1}{4}$D．a≤-1
2．$（3\frac{3}{8}）^{-\frac{2}{3}}-（5\frac{4}{9}）^{0.5}+$$（0.008）^{-\frac{2}{3}}×（0.02）^{\frac{1}{2}}$×$（0.32）^{\frac{1}{2}}$=$\frac{1}{3}$．
12．$\int_{-2}^2{\frac{1}{x+3}}dx$=ln5．
19．随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额），如下表：
年份20102011201220132014
储蓄存款y（千亿元）567810
（1）求y关于x的回归方程 $\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）用所求的回归方程预测该地区2015年的人民币储蓄存款．
注：$\left\{\begin{array}{l}b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}\right.$．
16．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x（x＞0）}\\{0（x=0）}\\{{x}^{2}+mx（x＜0）}\end{array}\right.$为奇函数．
（1）求f（-1）以及m的值；
（2）在给出的直角坐标系中画出y=f（x）的图象，并写出单调区间；
（3）就k的取值范围，讨论函数g（x）=f（x）-2k+1的零点个数．
17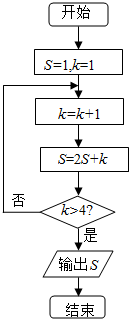．某程序框图如图所示，则输出的结果S等于（　　）
A．26B．57C．60D．61

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网