题目内容
12.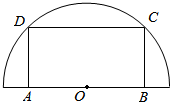 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.(1)设BC的长度为x,矩形ABCD的面积为y,试写出y关于x的函数关系式;
(2)求当BC多少时,矩形ABCD的面积最大,并求出该最大值.
分析 (1)连结OC,求出OB,然后求解表达式.
(2)利用基本不等式求出函数的最值即可.
解答  解:(1)连结OC,得$OB=\sqrt{900-{x^2}}$,所以AB=$2\sqrt{900-{x^2}}$,
解:(1)连结OC,得$OB=\sqrt{900-{x^2}}$,所以AB=$2\sqrt{900-{x^2}}$,
所以y=$2x\sqrt{900-{x^2}}$,x∈(0,30)….(8分)
(2)因为$2x\sqrt{900-{x^2}}≤{x^2}+900-{x^2}=900$.
即x2=900-x2,即x=$15\sqrt{2}$时取等号,此时ymax=900…(15分)
答:$BC=15\sqrt{2}$时,矩形ABCD的面积最大,最大为900cm2….(16分)
点评 本题考查函数的解析式的求法,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
17.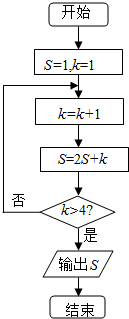 某程序框图如图所示,则输出的结果S等于( )
某程序框图如图所示,则输出的结果S等于( )
 某程序框图如图所示,则输出的结果S等于( )
某程序框图如图所示,则输出的结果S等于( )| A. | 26 | B. | 57 | C. | 60 | D. | 61 |
1.已知全集U={1,2,3,4,5,6},集合A={1,3,5,6},则∁UA等于( )
| A. | {1,3,5} | B. | {2,4,6} | C. | {2,4} | D. | {1,3,5,6} |