题目内容
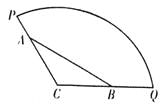
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
【答案】(1)![]() (2)当
(2)当![]() 两点各距
两点各距![]() 点60米处时,观光道路总长度达到最长,最长为
点60米处时,观光道路总长度达到最长,最长为![]() .
.
【解析】试题分析:(1)在![]() 中,由正弦定理易得
中,由正弦定理易得![]() 段的长度;(2)由题意,根据余弦定理可得
段的长度;(2)由题意,根据余弦定理可得![]() ,应用基本不等式可得当且仅当
,应用基本不等式可得当且仅当![]() 时,
时,![]() 取得最大值,
取得最大值,
试题解析:(1)在![]() 中,由已知及正弦定理得
中,由已知及正弦定理得![]() ,
,
即![]() ,∴
,∴![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
故![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 取得最大值,
取得最大值,
∴当![]() 两点各距
两点各距![]() 点60米处时,观光道路总长度达到最长,最长为
点60米处时,观光道路总长度达到最长,最长为![]() .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
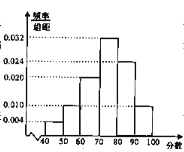
【题目】网络购物已经被大多数人接受,随着时间的推移,网络购物的人越来越多,然而也有部分人对网络购物的质量和信誉产生怀疑。对此,某新闻媒体进行了调查,在所有参与调查的人中,持“支持”和“不支持”态度的人数如下表所示:
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 (含50岁) | 100 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“支持”态度的人中抽取了9人,求
个人,已知从持“支持”态度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握认为支持网络购物与年龄有关?
参考数据:
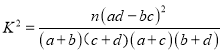 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |