题目内容
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
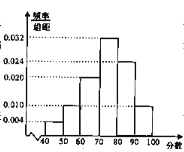
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
【答案】(1)860(2)75,75,74.2
【解析】
试题分析:(1)根据频率分布直方图可求得成绩不低于60分的概率值,结合样本容量可求得相应的人数;(2)众数为出现的次数最多的数,中位数为由小到大排列后的位于中间的数,平均数为各组的频率与该组的频数成绩之和
试题解析:(1)成绩不低于60分所占的频率为:1-(0.004+0.010)*10=0.86
所以成绩不低于60分的人数估计值为:1000*0.86=860(人) -----------4分
(2)众数估计值:75 ------------6分
设中位数为x,则(x-70)*0.032=0.5-0.04-0.1-0.2,解得x=75 ---------9分
平均数估计值:![]() s----12分
s----12分

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目