题目内容
12．已知数列{an}满足a1=1，an=an-1+2n（n≥2），则a7=（ ）| A． | 56 | B． | 55 | C． | 54 | D． | 53 |
分析 通过an=an-1+2n（n≥2）可知an-an-1=2n（n≥2），an-1-an-2=2（n-1），…，a2-a1=2•2，利用累加法计算即得结论．
解答 解：∵an=an-1+2n（n≥2），
∴an-an-1=2n（n≥2），
an-1-an-2=2（n-1），
…
a2-a1=2•2，
累加得：an-a1=2[2+3+…+n]
=2•$\frac{（n-1）（2+n）}{2}$
=n2+n-2，
∴an=a1+n2+n-2
=1+n2+n-2
=n2+n-1，
∴a7=72+7-1=55，
故选：B．
点评 本题考查数列的通项，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
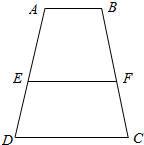在梯形ABCD中，AB=a，CD=b，a＜b，EF为一线段，若S四边形ABFE=S四边形CDEF，且∠BFE=∠D，求EF的长（用a，b表示）．