Question

7．如图，在四边形ABCD中，∠ABC=∠ADC=90°，∠DAB=60°，BD=6cm，求对角线AC的长．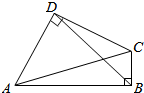

Answer 1

分析 利用∠ABC=∠ADC=90°，可得A、B、C、D四点共圆且AC直径，设AC的中点为O，连结DO并延交⊙O于点A′，∠A′=∠DAB=60°，利用三角函数，即可求对角线AC的长．

解答 解：∵四边形ABCD，∠ABC=∠ADC=90°，
∴A、B、C、D四点共圆且AC直径，
设AC的中点为O，连结DO并延交⊙O于点A′，则∠A′=∠DAB=60°，∠A′BD=90°．
Rt△A′BD中，BD=6（cm），∴AD=BD÷sinA=4$\sqrt{3}$，
∴AC=A′D=4√$\sqrt{3}$

点评 本题考查四点共圆，考查三角函数知识，确定A、B、C、D四点共圆且AC直径是关键．