题目内容
7．过已知双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左焦点F1作⊙O2：x2+y2=4的两条切线，记切点为A，B，双曲线的左顶点为C，若∠ACB=120°，则双曲线的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
分析 根据∠ACB=120°，OA=OC，可以得到∠AFO=30°，从而得到a与c的关系式，进而可求双曲线的离心率．
解答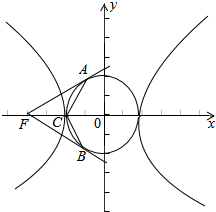 
解：因为∠ACB=120°，OA=OC，所以∠AOC=60°
∵FA是圆的切线，∴∠AFO=30°，
∴OF=2OC，
∴c=4，
∵a=2，
∴e=$\frac{c}{a}$=2
故选：D．
点评 本题考查双曲线的离心率，解题的关键是熟练掌握双曲线与圆的位置关系，结合有关条件确定a、b与c的关系．
练习册系列答案
相关题目
17．已知定点P在定圆O圆内或圆周上，圆C经过点P且与定圆O相切，则动圆C的圆心的轨迹是（ ）
| A． | 两条射线或圆或椭圆 | B． | 圆或椭圆或双曲线 | ||
| C． | 两条射线或圆或抛物线 | D． | 椭圆或双曲线或抛物线 |
已知，如图，已知PA和PB是⊙O的两条切线，PCD是⊙O的割线，弦AE∥PD，EB交CD于点F．求证：
2．
如图，AB是圆O的直径，P是AB延长线上的一点，过P作圆O的切线，切点为C，PC=$2\sqrt{3}$，若∠CAB=30°，则圆O的直径AB等于（ ）
如图，AB是圆O的直径，P是AB延长线上的一点，过P作圆O的切线，切点为C，PC=$2\sqrt{3}$，若∠CAB=30°，则圆O的直径AB等于（ ）| A． | 2 | B． | 4 | C． | 6 | D． | $2\sqrt{3}$ |