题目内容
14.一个正三棱柱的正视图是正方形,且它的外接球的表面积等于$\frac{25π}{3}$,则这个正三棱柱的底面边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{5\sqrt{7}}{7}$ | D. | 3 |
分析 由题设条件可得出正三棱柱的外接球半径、底面边长,由于其外接球的球心是棱柱上下底面的中点连线的中点Q,求出Q到棱柱顶点的距离即可求出球的半径,再由球的表面积公式求出球的表面积即可选出正确选项
解答 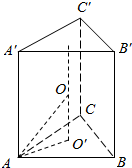 解:如图
解:如图
设三棱柱的棱长为a,则它的外接球球心O到底面距离为$\frac{1}{2}a$,
由已知设球半径为r,
∵外接球的表面积等于$\frac{25π}{3}$,
∴4πr2=$\frac{25π}{3}$,解得r2=$\frac{25}{12}$,
如图,O′A=$\frac{\sqrt{3}}{3}$a,O′A2+O′O2=r2=$\frac{{a}^{2}}{3}+\frac{{a}^{2}}{4}$,
∴a2=$\frac{25}{7}$,a=$\frac{5\sqrt{7}}{7}$
故选:C.
点评 本题考查了球的内接正三棱柱的问题;解决此类问题的关键是熟练掌握几何体的结构特征与及球的定义,在球的内接多面体中一般容易出现直角三角形,进而利用勾股定理解决问题即可.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.设z=1+i,则$\frac{2}{z}+{z^2}$=( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
19.曲线y=-x3+3x2在点(1,2)处的切线方程为( )
| A. | y=3x+5 | B. | y=-3x+5 | C. | y=3x-1 | D. | y=2x |
3.已知直线l经过点M(2,3),当l截圆(x-2)2+(y+3)2=9所得弦长最长时,直线l的方程为( )
| A. | x-2y+4=0 | B. | 3x+4y-18=0 | C. | y+3=0 | D. | x-2=0 |
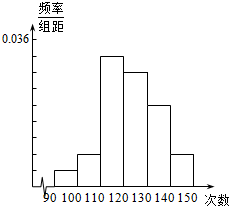 某校抽取一部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为1:2:8:7:5:2,第一小组频数为6.
某校抽取一部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为1:2:8:7:5:2,第一小组频数为6.