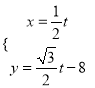题目内容
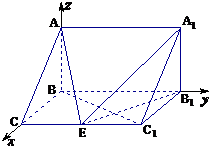
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1CC1 . 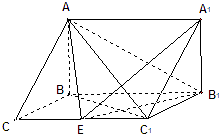
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1(要求说明理由).
(3)在(2)的条件下,若AB= ![]() ,求二面角A﹣EB1﹣A1的大小.
,求二面角A﹣EB1﹣A1的大小.
【答案】
(1)解:如图,以B为原点建立空间直角坐标系,则B(0,0,0),C1(1,2,0),B1(0,2,0)
直三棱柱ABC﹣A1B1C1中,
平面ABC的法向量 ![]() ,又
,又 ![]() ,
,
设BC1与平面ABC所成角为θ
,则 ![]()
(2)解:设E(1,y,0),A(0,0,z),则 ![]() ,
, ![]()
∵EA⊥EB1,
∴ ![]()
∴y=1,即E(1,1,0)所以E为CC1的中点
(3)解:∵A(0,0, ![]() ),则
),则 ![]() ,
,
设平面AEB1的法向量m=(x1,y1,z1),
则 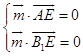 ∴
∴ 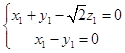 ,
,
取m=(1,1, ![]() ),
),
∵ ![]() ,
, ![]()
∴BE⊥B1E,又BE⊥A1B1∴BE⊥平面A1B1E,
∴平面A1B1E的法向量 ![]() ,
,
∴cos<m, ![]() >=
>= ![]() ,
,
∴二面角A﹣EB1﹣A1为45°.
【解析】(1)求出平面的法向量与直线所在的向量,利用向量的有关运算求出两个向量的夹角,进而转化为线面角即可.(2)根据点的特殊位置设出点的坐标为E(1,y,0),再利用向量的基本运算证明两个向量垂直即可证明两条直线相互垂直.(3)结合题意求出两个平面的法向量求出两个法向量的夹角,再转化为两个平面的二面角即可.
【考点精析】关于本题考查的用空间向量求直线与平面的夹角,需要了解设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: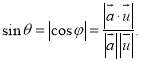 才能得出正确答案.
才能得出正确答案.

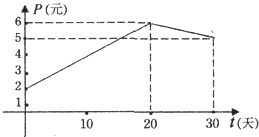
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?