题目内容
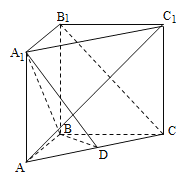
【题目】如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(Ⅰ)证明:AB1⊥平面A1B1C1;
(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.
【答案】(Ⅰ)见解析
(Ⅱ)![]()
【解析】分析:方法一:(Ⅰ)通过计算,根据勾股定理得![]() ,再根据线面垂直的判定定理得结论,(Ⅱ)找出直线AC1与平面ABB1所成的角,再在直角三角形中求解.
,再根据线面垂直的判定定理得结论,(Ⅱ)找出直线AC1与平面ABB1所成的角,再在直角三角形中求解.
方法二:(Ⅰ)根据条件建立空间直角坐标系,写出各点的坐标,根据向量之积为0得出![]() ,再根据线面垂直的判定定理得结论,(Ⅱ)根据方程组解出平面
,再根据线面垂直的判定定理得结论,(Ⅱ)根据方程组解出平面![]() 的一个法向量,然后利用
的一个法向量,然后利用![]() 与平面
与平面![]() 法向量的夹角的余弦公式及线面角与向量夹角的互余关系求解.
法向量的夹角的余弦公式及线面角与向量夹角的互余关系求解.
详解:方法一:
(Ⅰ)由![]() 得
得![]() ,
,
所以![]() .
.
故![]() .
.
由![]() ,
,![]()
![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() ,故
,故![]() .
.
因此![]() 平面
平面![]() .
.
(Ⅱ)如图,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连结
,连结![]() .
.
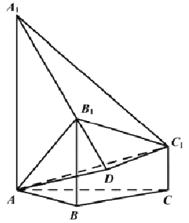
由![]() 平面
平面![]() 得平面
得平面![]() 平面
平面![]() ,
,
由![]() 得
得![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角.学科.网
所成的角.学科.网
由![]() 得
得![]() ,
,
所以![]() ,故
,故![]() .
.
因此,直线![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() .
.
方法二:
(Ⅰ)如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.
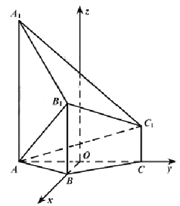
由题意知各点坐标如下:
![]()
因此![]()
由![]() 得
得![]() .
.
由![]() 得
得![]() .
.
所以![]() 平面
平面![]() .
.
(Ⅱ)设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
由(Ⅰ)可知![]()
设平面![]() 的法向量
的法向量![]() .
.
由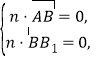 即
即![]() 可取
可取![]() .
.
所以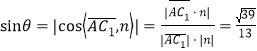 .
.
因此,直线![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() .
.

练习册系列答案
相关题目