题目内容
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.

求证:(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结论;
(2)由题意首先证得线面垂直,然后结合线面垂直证明线线垂直即可.
(1)因为D,E分别为BC,AC的中点,
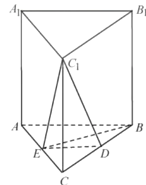
所以ED∥AB.
在直三棱柱ABC-A1B1C1中,AB∥A1B1,
所以A1B1∥ED.
又因为ED平面DEC1,A1B1![]() 平面DEC1,
平面DEC1,
所以A1B1∥平面DEC1.
(2)因为AB=BC,E为AC的中点,所以BE⊥AC.
因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC.
又因为BE平面ABC,所以CC1⊥BE.
因为C1C平面A1ACC1,AC平面A1ACC1,C1C∩AC=C,
所以BE⊥平面A1ACC1.
因为C1E平面A1ACC1,所以BE⊥C1E.

练习册系列答案
相关题目