题目内容
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
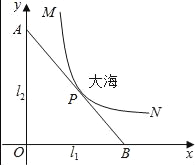
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
【答案】(1)见解析; (2)见解析.
【解析】
(1)由题意得M(1,8),则a=8,即得曲线段的函数关系式,可得其定义域;
(2)由函数关系式设点P坐标,设直线AB方程,将直线方程与曲线方程联立求出A,B坐标,即可求出最短长度p的取值范围
(1)由题意得M(1,8),则a=8,故曲线段MPN的函数关系式为![]() ,
,
又得![]() ,所以定义域为[1,10].
,所以定义域为[1,10].
(2)![]() ,设AB:
,设AB:![]()
由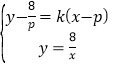 得kpx2+(8﹣kp2)x﹣8p=0,
得kpx2+(8﹣kp2)x﹣8p=0,
△=(8﹣kp2)2+32kp2=(kp2+8)2=0,
∴kp2+8=0,∴![]() ,得直线AB方程为
,得直线AB方程为![]() ,
,
得![]() ,B(2p,0),故点P为AB线段的中点,
,B(2p,0),故点P为AB线段的中点,
由![]() 即p2﹣8>0,
即p2﹣8>0,
得![]() 时,OA<OB,
时,OA<OB,
所以,当![]() 时,经点A至P路程最近.
时,经点A至P路程最近.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目