题目内容
(本小题满分12分)已知椭圆: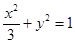 ,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.
,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.
(I)求证O到直线AB的距离为定值.
(Ⅱ)求△0AB面积的最大值.
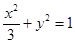 ,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.
,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.(I)求证O到直线AB的距离为定值.
(Ⅱ)求△0AB面积的最大值.
解:(Ⅰ) 设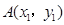 ,
, ,若k存在,则设直线AB:y=kx+m.
,若k存在,则设直线AB:y=kx+m.
由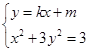 ,得
,得
△ >0, …2分有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)
…2分有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)
=(1+k2) x1x2+k m(x1+x2)=0 ………4分
代入,得4 m2=3 k2+3原点到直线AB的距离d= .……5分
.……5分
当AB的斜率不存在时, ,可得
,可得 ,依然成立.
,依然成立.
所以点O到直线 的距离为定值
的距离为定值 .………………6分
.………………6分
(Ⅱ) …………8分
…………8分
= =
= ≤4
≤4
当且仅当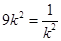 ,即
,即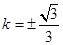 时等号成立.………………10分
时等号成立.………………10分
当斜率不存在时,经检验|AB|<2.所以 ≤
≤ .…12分
.…12分
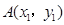 ,
, ,若k存在,则设直线AB:y=kx+m.
,若k存在,则设直线AB:y=kx+m.由
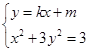 ,得
,得
△ >0,
 …2分有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)
…2分有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)=(1+k2) x1x2+k m(x1+x2)=0 ………4分
代入,得4 m2=3 k2+3原点到直线AB的距离d=
 .……5分
.……5分当AB的斜率不存在时,
 ,可得
,可得 ,依然成立.
,依然成立.所以点O到直线
 的距离为定值
的距离为定值 .………………6分
.………………6分(Ⅱ)
 …………8分
…………8分=
 =
= ≤4
≤4当且仅当
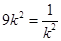 ,即
,即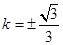 时等号成立.………………10分
时等号成立.………………10分当斜率不存在时,经检验|AB|<2.所以
 ≤
≤ .…12分
.…12分略

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
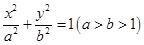 内有圆
内有圆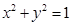 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足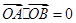 (其中
(其中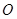 为坐标原点).
为坐标原点).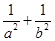 为定值;
为定值;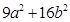 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程;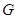 的中心在坐标原点,其中一个焦点为圆
的中心在坐标原点,其中一个焦点为圆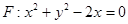 的圆心,右顶点是圆F与x轴的一个交点.已知椭圆
的圆心,右顶点是圆F与x轴的一个交点.已知椭圆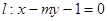 相交于A、B两点.
相交于A、B两点. )求
)求 椭圆的方程;
椭圆的方程;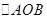 面积的最大值;
面积的最大值;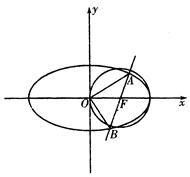
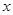 轴上,焦距为8,且经过点(0,3)
轴上,焦距为8,且经过点(0,3)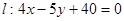 ,问:椭圆C上是否存在一点,使它到直线
,问:椭圆C上是否存在一点,使它到直线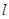 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?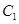 :
: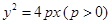 ,焦点为
,焦点为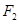 ,其准线与
,其准线与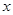 轴交于点
轴交于点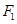 ;椭圆
;椭圆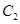 :分别以
:分别以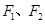 为左、右焦点,其离心率
为左、右焦点,其离心率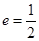 ;且抛物线
;且抛物线 的一个交点记为
的一个交点记为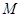 .
.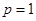 时,求椭圆
时,求椭圆
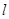 经过椭圆
经过椭圆 与抛物线
与抛物线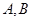 两点,若弦长
两点,若弦长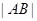 等于
等于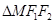 的周长,求直线
的周长,求直线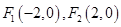 ,一曲线
,一曲线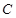 经过点
经过点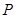 ,且
,且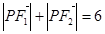
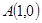 ,若
,若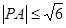 ,求点
,求点
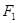 、
、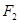 是椭圆
是椭圆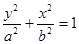
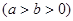 的左、右焦点,
的左、右焦点,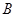 是该椭圆短轴的一个端点,直线
是该椭圆短轴的一个端点,直线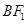 与椭圆
与椭圆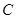 交于点
交于点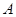 ,若
,若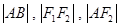 成等差数列,则该椭圆的离心率为
成等差数列,则该椭圆的离心率为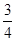
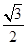
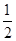
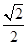
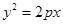 的焦点与椭圆
的焦点与椭圆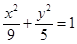 的左焦点重合,则
的左焦点重合,则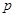 的值为_________
的值为_________