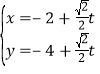题目内容
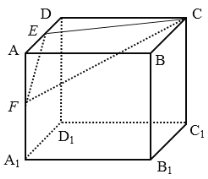
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则以下说法错误的是( )
的中点,则以下说法错误的是( )
A.平面![]() 截正方体所的截面周长为
截正方体所的截面周长为![]()
B.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
C.三棱锥![]() 和
和![]() 体积相等
体积相等
D.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
【答案】B
【解析】
对于A,平面![]() 截正方体所得的截面为梯形
截正方体所得的截面为梯形![]() ,求出梯形的周长即可得解;
,求出梯形的周长即可得解;
对于B,通过建立空间直角坐标系,设出![]() 点坐标,证出
点坐标,证出![]() 不成立,即可得出B选项错误;
不成立,即可得出B选项错误;
对于C,通过等体积法,分别求出三棱锥![]() 和
和![]() 的体积,进而得解;
的体积,进而得解;
对于D,通过线线平行,证得线面平行,进而得解.
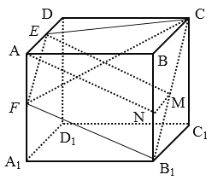
对于A选项,连接![]() ,
,![]() ,
,
![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 四点共线,
四点共线,
![]() 平面
平面![]() 截正方体所得的截面为梯形
截正方体所得的截面为梯形![]() ,
,
![]() 截面周长
截面周长![]() ,
,
故A正确;
对于B选项,建立如图所示的空间直角坐标系,
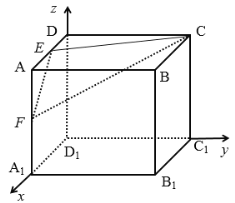
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
所以![]() ,
,![]() ,
,
若![]() 平面
平面![]() ,则
,则![]() ,而
,而![]() 显然不成立,
显然不成立,
所以![]() 与
与![]() 不垂直,所以
不垂直,所以![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() ,
,
所以B选项错误;
对于C选项,
![]() ,
,
![]() ,
,
所以![]() 成立,C正确;
成立,C正确;
对于D选项,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 点
点![]() 为
为![]() 的中点,
的中点,
![]()
![]() 上存在一点
上存在一点![]() 使得
使得![]() 平面
平面![]() ,故D正确.
,故D正确.
故选:B.

练习册系列答案
相关题目
【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
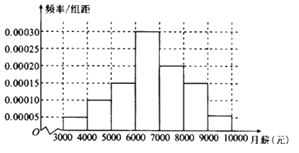
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
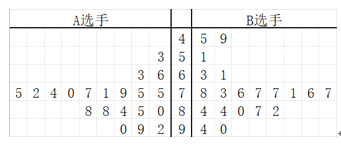
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.