题目内容
【题目】根据要求求值:
(1)用辗转相除法求123和48的最大公约数.
(2)用更相减损术求80和36的最大公约数.
(3)把89化为二进制数.
【答案】
(1)解:辗转相除法求最大公约数的过程如下:
123=2×48+27,48=1×27+21,27=1×21+6,21=3×6+3,6=2×3+0,
最后6能被3整除,得123和48的最大公约数为3
(2)解:我们将80作为大数,36作为小数,因为80和36都是偶数,要除公因数2.
80÷2=40,36÷2=18.40和18都是偶数,要除公因数2.40÷2=20,18÷2=9.
求20与9的最大公约数,20﹣9=11,11﹣9=2,9﹣2=7,7﹣2=5,5﹣2=3,3﹣2=1,
2﹣1=1,可得80和36的最大公约数为22×1=4.
(3)解:如图所示,可得:89(10)=1 011 001(2).
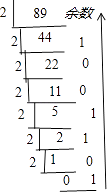
【解析】(1)利用辗转相除法即可得出;(2)我们将80作为大数,36作为小数,因为80和36都是偶数,要除公因数2.依此类推可得:80÷4=20,36÷4=9.利用更相减损术求20与9的最大公约数,即可得出.(3)如图所示,即可得出.
【考点精析】本题主要考查了进位制的相关知识点,需要掌握进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值才能正确解答此题.

【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
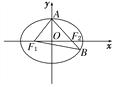
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.