题目内容
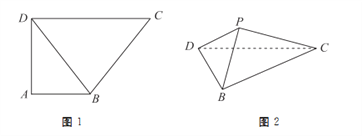
【题目】已知直角梯形
中， 
， 
， 
， 
， 
，如图1所示，将
沿
折起到
的位置，如图2所示.
（1）当平面
平面
时，求三棱锥
的体积；
（2）在图2中， 
为
的中点，若线段
，且
平面
，求线段
的长；
【答案】（1）
（2）1
【解析】试题分析：（1）由面面垂直性质定理得
平面
，即为三棱锥
的高，再根据三棱锥体积公式求体积（2）取
的中点
，则根据三角形中位线性质得
，即得
，再根据线面平行性质定理得
.即得四边形
是平行四边形.可得
.
试题解析：（1）当平面
平面
时，因为
，且平面
平面
， 
平面
，所以
平面
，因为
平面
，所以
.因为在直角梯形
中， 
， 
， 
， 
， 
，所以
， 
.所以
.又因为
，所以
，所以
.所以
.所以三棱锥
的体积等于
.
（2）取
的中点
，连接
， 
，如上图所示.又因为
为
的中点，所以
，且
.又因为
，所以
.所以
， 
， 
， 
共面.因为
平面
， 
平面
，且平面
平面
，所以
.又因为
，所以四边形
是平行四边形.所以
.
点睛: 将平面图形沿其中一条或几条线段折起，使其成为空间图形，把这类问题称为平面图形的翻折问题．平面图形经过翻折成为空间图形后，原有的性质有的发生了变化，有的没有发生变化，弄清它们是解决问题的关键．一般地，翻折后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化．解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值，这是化解翻折问题难点的主要方法．立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.
练习册系列答案
相关题目
【题目】2015年12月，京津冀等地数城市指数“爆表”，北方此轮污染为2015年以来最严重的污染过程，为了探究车流量与
的浓度是否相关，现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的数据如表：
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
（1）由散点图知
与
具有线性相关关系，求
关于
的线性回归方程；
的浓度；
（ii）规定：当一天内
的浓度平均值在
内，空气质量等级为优；当一天内
的浓度平均值在
内，空气质量等级为良，为使该市某日空气质量为优或者为良，则应控制当天车流量在多少万辆以内？（结果以万辆为单位，保留整数）
参考公式：回归直线的方程是
，其中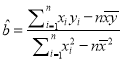
， 
.
