题目内容
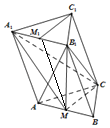
【题目】在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.
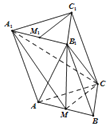
(1)求证:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B为正三角形,AB=2,BC=1,![]() ,求四棱锥B1﹣AA1C1C的体积.
,求四棱锥B1﹣AA1C1C的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连结M1M,推导出四边形MCC1M1是平行四边形,从而C1M1∥CM,由此能证明C1M1∥面A1MC.
(2)推导出B1M⊥AB,B1M⊥面ABC,B1M是三棱柱ABC﹣A1B1C1的高,四棱锥B1﹣AA1C1C的体积为![]() .
.
(1)连结M1M,
∵在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.
∴M1M∥B1B,且M1M=B1B,C1C∥B1B,且C1C=B1B,
∴M1M∥C1C,且M1M=C1C,
∴四边形MCC1M1是平行四边形,
∴C1M1∥CM,
∵C1M1![]() 平面A1MC,CM平面A1MC,
平面A1MC,CM平面A1MC,
∴C1M1∥面A1MC.
(2)∵△ABB1是正三角形,面ABC⊥面ABB1A1,M为AB中点,
∴B1M⊥AB,∴B1M⊥面ABC,
∴B1M是三棱柱ABC﹣A1B1C1的高,
∵AB=2,BC=1,![]() ,∴BC2+AC2=AB2,∴∠ACB=90°,
,∴BC2+AC2=AB2,∴∠ACB=90°,
∴四棱锥B1﹣AA1C1C的体积为:
![]() sh
sh![]() sh
sh![]() 1.
1.

【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 周长为8.
周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() ,使以
,使以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,若存在求出直线
,若存在求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;
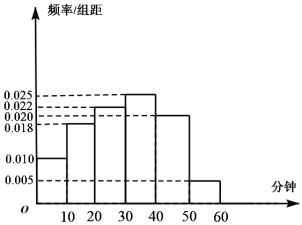
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别
列联表,并据此资料你是否认为“体育迷”与性别
有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
| 0.05 | 0.01 |
k | 3.841 | 6.635 |
附![]()
【题目】平行志愿投档录取模式是高考志愿的一种新方式,2008年教育部在6个省区实行平行志愿投档录取模式的试点改革.一年的实践证叨,实行平行志愿投档录取模式,有效降低了考生志愿填报风险.平行志愿是这样规定:在同一批次设置几个志愿,当考生分数达到这几个学校提档线时,本批次的志愿依次检索录取.某考生根据对自己的高考分数和对往年学校录取情况分析,从报考指南中选择了10所学校,作出如下表格:
学校 |
|
|
|
|
|
|
|
|
|
|
专业 | 数学系 | 计算机系 | 物理系 | |||||||
录取概率 | 0.5 | 0.5 | 0.6 | 0.9 | 0.5 | 0.7 | 0.8 | 0.7 | 0.8 | 0.9 |
(1)该考生从上表中的10所学校中选择4所学校填报,记![]() 为选择的4所学校中报数学系专业的个数,求
为选择的4所学校中报数学系专业的个数,求![]() 的分布列及其期望
的分布列及其期望![]() ;
;
(2)若该考生选择了![]() 、
、![]() 、
、![]() 、
、![]() 这4个学校在同一批次填报志愿,填报志愿表如下,如果仅以该考生对自己分析的录取概率为依据,当改变这4个志愿填报的顺序时,是否改变他本批次录取的可能性?请说明理由.
这4个学校在同一批次填报志愿,填报志愿表如下,如果仅以该考生对自己分析的录取概率为依据,当改变这4个志愿填报的顺序时,是否改变他本批次录取的可能性?请说明理由.
志愿 | 学校 |
第一志愿 | |
第二志愿 | |
第三志愿 | |
第四志愿 |