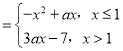题目内容
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
【答案】(1)切线方程![]() ;
;![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(I)函数求导![]() ,求出
,求出![]() 得切线方程;解
得切线方程;解![]() 求单增区间,解
求单增区间,解![]() 求单减区间;利用单调性求最值;
求单减区间;利用单调性求最值;
(II)构造![]() 得到函数调调性,由零点存在性定理证有且只有一个零点.
得到函数调调性,由零点存在性定理证有且只有一个零点.
(I)当![]() 时,
时,
①函数![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 曲线
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
②令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单增,在
上单增,在![]() 单减,
单减,
![]() 函数
函数![]() 的最小值为
的最小值为![]() .
.
(II) 当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
等价于![]() 有且只有一个零点.
有且只有一个零点.
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单增,
上单增,
又![]() ,
,
![]() ,
,
由零点存在性定理得![]() 有唯一零点,即曲线
有唯一零点,即曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.

练习册系列答案
相关题目
【题目】在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(1)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(2)从上表三个社区的志愿者中各任取1人调查情况,以X表示负责现场值班值守的人数,求X的分布列;
(3)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询满意,“
”分别表示A,B,C社区的人们对心理咨询满意,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询不满意,写出方差
”分别表示A,B,C社区的人们对心理咨询不满意,写出方差![]() ,
,![]() ,
,![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)