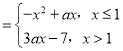题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,讨论函数
,讨论函数![]() 的单调性与单调区间;
的单调性与单调区间;
(Ⅲ)若![]() 有两个极值点
有两个极值点![]() 、
、![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析;(Ⅲ)证明见解析.
;(Ⅱ)详见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)求出![]() 和
和![]() 的值,利用点斜式可得出所求切线的方程;
的值,利用点斜式可得出所求切线的方程;
(Ⅱ)求得![]() ,由
,由![]() ,分
,分![]() 和
和![]() 两种情况讨论,分析
两种情况讨论,分析![]() 的符号变化,可得出函数
的符号变化,可得出函数![]() 的单调递增区间和递减区间;
的单调递增区间和递减区间;
(Ⅲ)由题意可知,方程![]() 有两正根
有两正根![]() 、
、![]() ,利用韦达定理得出
,利用韦达定理得出![]() ,
,![]() 且
且![]() ,将所证不等式转化为
,将所证不等式转化为![]() ,构造函数
,构造函数![]() ,利用导数证明出当
,利用导数证明出当![]() 时,
时,![]() 即可.
即可.
由题可知:函数![]() 的定义域为
的定义域为![]()
(Ⅰ)因为![]() 时,
时,![]() ,所以
,所以![]() ,
,
那么![]() ,
,![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() ,
,
即![]() ;
;
(Ⅱ)因为![]() ,由
,由![]() 可得:
可得:
①当![]() ,
,![]() ,时,有
,时,有![]() ,
,![]() ,满足
,满足![]() ,
,
![]() 和
和![]() 时
时![]() ,
,
即函数![]() 在
在![]() 和
和![]() 上为减函数;
上为减函数;
![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 上为增函数;
上为增函数;
②当![]() 时,
时,![]() ,
,![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 为减函数.
为减函数.
综上可知:
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上为减函数,
上为减函数,
在![]() 上为增函数;
上为增函数;
当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数;
上为减函数;
(Ⅲ)因为![]() 有两个极值点
有两个极值点![]() 、
、![]() ,
,
则![]() 有两个正根
有两个正根![]() 、
、![]() ,则有
,则有![]() ,且
,且![]() ,
,![]() ,即
,即![]() ,
,
所以![]()
若要![]() ,即要
,即要![]() ,
,
构造函数![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上为增函数,
上为增函数,
且![]() ,
,![]() ,
,
所以存在![]() 使
使![]() 即
即![]() ,
,
且当![]() 时
时![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
所以函数![]() 在
在![]() 上有最小值为
上有最小值为 ,
,
又因为![]() 则
则![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3