题目内容
19.为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:| 分组 | 频数累计 | 频数 | 频率 |
| [10.75,10.85) | 6 | 6 | 0.06 |
| [10.85,10.95) | 15 | 9 | 0.09 |
| [10.95,11.05) | 30 | 15 | 0.15 |
| [11.05,11.15) | 48 | 18 | 0.18 |
| [11.15,11.25) | |||
| [11.25,11.35) | 84 | 12 | 0.12 |
| [11.35,11.45) | 92 | 8 | 0.08 |
| [11.45,11.55) | 98 | 6 | 0.06 |
| [11.55,11.65) | 100 | 2 | 0.02 |
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在[10.95,11.35)范围内的可能性是百分之几?
(Ⅳ)从[11.35,11.45)∪[11.55,11.65)中抽取两个产品,直径分别记作为x,y,求|x-y|<0.1的概率

分析 (Ⅰ)由题意根据频率分步表的性质,可得完整的频率分步表.
(Ⅱ)根据完整的频率分步表,画出频率分布直方图.
(Ⅲ)据上述图表,求出产品直径落在[10.95,11.35)范围内的频率,即为所求.
(Ⅳ)所有的抽法有${C}_{10}^{2}$=45种,其中满足条件的抽法有${C}_{8}^{2}$+${C}_{2}^{2}$=29种,由此可得所求事件的概率.
解答 解:(Ⅰ)由题意根据频率分步表的性质,可得完整的频率分步表:
| 分组 | 频数累计 | 频数 | 频率 |
| [10.75,10.85) | 6 | 6 | 0.06 |
| [10.85,10.95) | 15 | 9 | 0.09 |
| [10.95,11.05) | 30 | 15 | 0.15 |
| [11.05,11.15) | 48 | 18 | 0.18 |
| [11.15,11.25) | 72 | 24 | 0.24 |
| [11.25,11.35) | 84 | 12 | 0.12 |
| [11.35,11.45) | 92 | 8 | 0.08 |
| [11.45,11.55) | 98 | 6 | 0.06 |
| [11.55,11.65) | 100 | 2 | 0.02 |
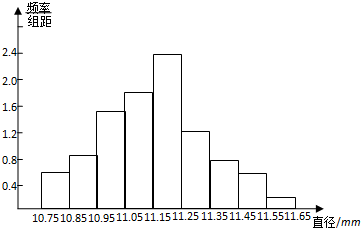
(Ⅲ)据上述图表,产品直径落在[10.95,11.35)范围内的频率为 0.15+0.18+0.24+0.12=0.69=69%,
估计产品直径落在[10.95,11.35)范围内的可能性为69%.
答:略.
(Ⅳ)所有的抽法有${C}_{10}^{2}$=45种,其中满足条件的抽法有${C}_{8}^{2}$+${C}_{2}^{2}$=29种,
故|x-y|<0.1的概率为 $\frac{29}{45}$.
点评 本题主要考查频率分步表的性质,频率分步直方图的画法,古典概率的计算公式,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
10.已知点P是边长为4的正方形内任一点,则点P到四个顶点的距离均大于2的概率是( )
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |

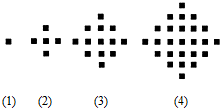 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.